Vascular Architecture in Plants

Prerequisites: Water Transport in plants; structure of wood.

Vascularisation is essential for any large land plant. Water, carrying mineral nutrients from the soil need to travel from the roots to other parts of the plant in the xylem vessels, whilst sugary sap must, for example, translocate from photosynthesizing leaves and storage organs to growing parts and ripening fruit in phloem vessels. Plants are often divided into vascular and non-vascular, which roughly parallels evolution with large terrestrial forms appearing later in evolution as vessels evolved sufficiently to supply their needs. However, this division is a simplification. Seaweeds might not require xylem, since they can absorb water across their entire body surface when submerged, but they do have a well-developed network of phloem vessels, called trumpet hyphae, interconnecting the various parts of the seaweed body. Mosses are tiny and although terrestrial, many require damp conditions and so it is not surprising that they do not require advanced vascular systems. However, even small mosses may have specialized conducting tissue, functioning as a prototype vascular system.

Above: primary plant stem vascular tissue in cross-section. Primary stems are generally green and photosynthetic and have no or little secondary growth and so are non-woody and occur in young shoots and in herbaceous plants. This diagram illustrates the structure of the vascular cylinder or stele (surrounding stem tissues are not shown). White indicates phloem, xylem is shown in black and central parenchymatous pith is dotted. Protosteles occur in many fossil plants, in psilopsids and club mosses and in some roots. In these steles there is a central solid cylinder of xylem ensheathed by phloem. For example, the psilopsid Psilotum nudum has an actinostele (in which the xylem cylinder is ridged) and the club moss Lycopodium clavatum has a plectostele, in which plates of phloem infiltrate the xylem, which is nevertheless still continuous.

Xylem has to be rigid so that it can draw up sap under suction pressure without collapsing. This makes xylem good for plant support and in woody plants it is the main supporting or skeletal tissue. To provide greater support without manufacturing more expensive xylem, the plant stem can contain a hollow cylinder of xylem. Just as in the hollow long bones of mammals, it is possible to have a bone which contains less bony material but which is nevertheless stronger, as in having greater flexural stiffness - a wide cylinder is much harder to bend than a narrow cylinder, though we have to maintain a minimum thickness of the walls of the hollow cylinder to prevent buckling. This gives rise to a siphonostele, in which the vascular tissue forms a hollow cylinder or siphon, although the central cavity may be filled with parenchymatous pith. In the ectophloic siphonostele in which the phloem remains on the outside surface of the xylem or an amphiphloic siphonostele (also called a solenostele) in which phloem coats both the inner and outer surface of the xylem cylinder. Siphonosteles occur in ferns, and in some gymnosperms and flowering plants.

The vascular cylinder is not generally a complete cylinder, because at the leaf-bearing nodes of the stem xylem and phloem vessels must arc away from the stele to enter the leaf as a leaf trace. If the leaf is a small scale-like leaf or microphyll, the vascular cylinder may remain more-or-less intact, otherwise, if a larger trace enters a large leaf or macrophyll a gap may result in the xylem cylinder, called a leaf gap. This gap only extends so far up the cylinder before the cylinder closes over at the internode above to become a complete circle again in cross-section.

Above: left, the complete vascular cylinder (siphonostele) of an internode. Middle, a small vascular trace arcs away from the stele to enter a microphyll, leaving a notch in the vascular cylinder which extends part-way up. Right, a leaf trace entering a macrophyll results in a gap, or elongated slit, in the vascular cylinder, called a leaf gap.

In the dictyostele we essentially have a modified siphonostele in which the stem has very short internodes, so that leaf gaps of the nodes above and below overlap to completely and in cross-section the stele appears to be broken up into a series of strands. This type of stele occurs in some ferns.

In the eustele (literally 'true stele') the vascular tissue is broken up into discrete longitudinal strands or bundles. This type of stele occurs in the internodes of the horsetail Equisetum and in some gymnosperms and flowering plants. It is the 'typical dicotyledonous' primary stem illustrated in text books, e.g. Helianthus.

Finally, in the atactostele we have the discrete bundles of vascular tissue scattered throughout the stem. This type of stem is characteristic of monocotyledonous flowering plants.

Secondary Growth

After attaining their initial width and length, the parts of many plants undergo secondary growth, increasing in
thickness and strength. New secondary xylem and phloem will be produced to supply the growing plant. The covering of the epidermis may become replaced with periderm bearing 'breathing pores' or lenticels. In a eustele, a layer of undifferentiated cells between the phloem and xylem of each vascular bundle (fascicle) my form a growth zone or meristem where new cells are produced. This is called the fascicular cambium and is continuous with a layer of similar cells inbetween the vascular bundles, the interfascicular cambium. Thus there is a complete cylinder of meristematic tissue only one or a few cell layers thick.As these cells divide by mitosis, they both replace themselves to maintain the meristem and produce cells which differentiate into new xylem vessels on the inside of the stele and new phloem on the outside.

This type of secondary growth is extensive in woody plants and indefinite in many trees, with the secondary xylem forming the wood and the secondary phloem the innermost layer of the bark (or just beneath the bark proper). Herbaceous plants may also undergo some secondary growth, depending on species. In  Pelargonium (Geraniaceae) the vascular bundles are so close together that secondary growth readily produces an entire fused cylinder of vascular tissue. In Helianthus (sunflower, Asteraceae) a similar continuous cylinder may form at the base of the stem, but higher up there is no secondary growth, but the interfascicular parenchyma (parenchyma inbetween the vascular bundles) forms sclerenchyma to toughen the stem and give it extra strength. A periderm may not form in Helianthus, but the epidermis continues to produce new cells and expand.

As has been discussed elsewhere (see wood) trees often grow by adding annual rings of wood such that the stem increases in girth. If we picture a tree stem as consisting of a cone of wood then essentially a new cone is added over the top of this each year or growing season.

 Review the detailed structure and function of wood and xylem vessels.

In this article we will look at some additional features of xylem architecture in trees. A single xylem vessel does not generally extend the whole height of the tree but may be a meter or so in length and communicates with neighbouring vessels so that the sap can flow the whole height of the tree from vessel to vessel. The xylem sap is drawn up the tree from the roots by a suction pressure generated by water loss, chiefly through stomata in the leaves of the tree canopy. This loss of water to the atmosphere is transpiration and the stream of water flowing through the xylem, carrying valuable mineral salts from the soil, is called the transpiration stream. This does mean, however, that the lower branches are nearer the source of the flowing sap and may tap more than their fair share, leaving insufficient sap for the upper canopy which potentially needs it more. To combat this trees have a special architectural feature to slow the movement of xylem sap into the lower branches - concentric circular vessels.

Above: the grain in a tree with its bark removed. Note the concentric circular or elliptical vessels at the bases of the lower branches.

An important part of a tree's insurance policy is the production of dormant buds. Most of these buds will never open or develop, but should the canopy become damaged some of them may become active and replace the damaged canopy. Each dormant bud has its own vascular supply which must elongate if the bud is to remain at the surface of the stem as an epicormic bud. As new layers of wood are added to the trunk, the vascular traces to the buds elongate to maintain the buds at the surface (some buds may fail to keep up and become buried in the wood).

Above: a longitudinal section of a tree trunk showing the vascular supply to the dormant epicormic buds. (Based on Busgen and Munch, 1929, in Thomas,2000; trees: their natural history, Cambridge University Press).

Epicormic buds originally form as normal buds in the axils of leaves on young sheets but which remain dormant. In some trees the majority of such buds remain dormant and some may abort. Trees can also form new buds de nova when they are damaged, from any parenchyma tissue (adventitious buds).  Branches also have vascular traces which can be traced to the centre of the trunk as a narrowing cone (a 'spike knot'). As new wood is added the growth of the branch keeps pace and the knot consists entirely of wood firmly anchored to the surrounding wood of the trunk. However, if the branch dies then wood added to the trunk will simply grow over it, encasing the dead branch complete with its bark. The bark around the dead wood does not integrate well and such encased knots easily fall out of a plank of cut wood.

Hydraulic Architecture

The physics of water movement in plants and how plants control this is a very complicated subject! However, an understanding of this topic sheds considerable light on plant anatomy and physiology, including the reasons why conifers and hard woods have different types of wood, for example. Here we will discuss some of the principles and results of published studies. This section will probably be expanded periodically to include additional material.

The mechanics of water transport in plants can be modeled using Ohm's law for electrical circuits, namely that the rate of flow (current) is equal to the 'driving force' (voltage) divided by the resistance. (Note we are using the word 'force' in a colloquial rather than a physical sense). Increasing the resistance reduces the rate of flow, whilst increasing the 'driving force' increases flow rate. In the case of the plant, we are of course concerned with the flow of water rather than the flow of electricity. The 'driving force' of water flow is pressure (rather than voltage) or the pressure gradient (pressure per meter).  

Note that the units for pressure are Pa which is equivalent to force per unit area, and that of the pressure gradient are Pa/m and so this is not a force in the strict physical sense. Conductance is used more often than resistance in plant physiology. Conductance is simply the reciprocal of resistance (conductance: k = 1/resistance).

Flow rate can be measured in terms of the mass of water passing a given point each second, i.e. the mass flow rate in kg/s; or in terms of the volume flow rate in meters cubed / s. The flow rate is given by:

   Flow rate = Pressure  x  Conductance

   Units: kg/s = Pa  x  kg/Pa/s

Or by:

   Flow rate = Pressure gradient  x  conductivity

   Units: kg/s = Pa/m  x  (kg/Pa/s)m

Where conductivity is conductance x length of the pipe (similarly resistivity is resistance  x  length).

Another way to look at this is to say that flow rate is proportional to pressure, with conductance as the constant of proportionality, or that flow rate is proportional to pressure gradient with conductivity the constant of proportionality. Thus, for example we have the following definition of conductivity:

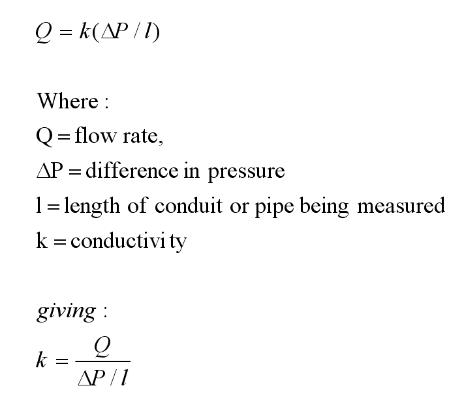
If Q, the flow rate of water, is given in kg/s, for example, and pressure in Pa (pascals) then the units of k will be:
(kg/s) / (Pa/m). Often pressure is inputted into this equation in MPa, but it is generally better practice to stick to SI
units.

We may be considering flow along an individual xylem vessel or along an entire branch. There is one further modification, we often talk in terms of leaf-specific (hydraulic) conductance (LSC) when considering flow along a stem segment. This is the conductivity of that stem segment divided by the total surface area of leaves irrigated by the same stem segment. This gives us a measure of how readily water can be supplied to the leaves. For example, the LSC of a stem will incorporate all the leaves supplied by that stem (i.e. the leaves downstream of the stem), but for a branch it will include only those leaves supplied by that branch. This gives us a measure of how well the axis (stem or branch) can supply its leaves with water.

Somebody probably ought to invent a name for the awkward units of hydraulic conductance.

Efficiency of water transport

Why do the leaves need so much water? If it was the case that they only needed a set amount then plant hydraulics would be tuned to supply that amount. However, the water rising in the xylem brings mineral nutrients absorbed by the roots to the cells of the leaf. Leaves also need to obtain carbon dioxide from the air through pores in the leaves called stomata. This necessarily exposes the interior of the leaf to the outside air causing water loss by evaporation (evapotranspiration). This water loss creates the suction (negative pressure gradient) which is mainly responsible for driving water up the xylem in the transpiration stream in the first place. Transpiration is necessary to replace the water lost so that the cells can maintain access to carbon dioxide (if the leaf wilts the stomata close and photosynthesis shuts down). For these reasons, conductivity correlates well to plant growth.

Murray's Law

Opposing the need for higher conductance are several costs. One of these is the cost of manufacturing the vascular system. Murray analyzed the blood circulatory systems of vertebrates and devised Murray's Law which states that blood vessels taper when they branch so as to maintain a flow rate, Q, proportional to the sum of the cubes of the radii of all the branches at every branch level in order to maximize conductance for a given investment in vascular tissue. That is:

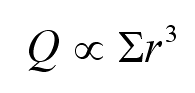
If we assume that flow rate is constant throughout the system (i.e. no fluid enters or leaves the system and the flow is steady) then this equates to requiring the sum of the radii cubed of branches of any order being equal to the same constant. That is, if a parent vessel branches into several daughter branches, then the sum of the cubed radii of the daughter branches is equal to the radius cubed of the parent vessel.

This proportionality can be derived from the (Hagen-)Poiseuille law for laminar (i.e. non-turbulent) flow in a cylindrical pipe and the assumption that power consumed (i.e. the rate of energy consumption) is minimised. This power is equal to the power used to drive the flow and the power used to maintain the circulatory system. It is further assumed that, for animals, the main maintenance cost is in production and maintenance of the blood itself, rather than the vessel walls (which are thin in all but the larger arteries). This means that the power for maintenance is proportional to the volume of the vessel. Vessels are assumed to be cylindrical. The derivation is given below for those who are curious:

Application of Murray's Law to Plants

The circulatory systems of plants are fundamentally very different to those of vertebrates. These differences can
be summarised in three key principles with specific reference to xylem:

1. Redundancy
   
2. Integration
   
3. Compartmentation
   

Redundancy. In plants, individual conducting channels or pipes (tracheids or xylem vessels) are in parallel bundles with the side-walls connected by pits (and pit fields). This means that flow can divert sideways from one pipe to another (even though the main flow is still along the pipe). This means that there is a high level of redundancy in the system: blockage of one pipe can be circumvented. This is functionally important, since in plants the conducting pipes of the xylem are under negative pressure and will sometimes cavitate (become blocked by air bubbles) or branches may become damaged by the elements or by grazing herbivores.

Integration. The xylem system of plants is highly integrated: each root is connected to and supplies all branches. This is partly a result of redundancy.

Compartmentation. The xylem system rarely consists of freely open pipes along the whole length of the plant. More typically vessels may extend a few cm or m before connecting to another vessel, perhaps sideways. Tracheids are typically only 1-2 (occasionally up to 10) mm long. This means that if air enters one compartment, then it can be contained and stopped from spreading to other compartments.

We also need to consider how the power required for maintenance differs for plants. The xylem sap is largely water and dissolved minerals drawn up from the roots and is assumed to have a low cost of manufacture (however roots do actively expend energy in transporting minerals into the xylem sap). The greater investment comes from the relatively thick walls of xylem conduits, which must be rigid to resist collapse since the xylem operates under negative pressure (suction) rather than positive pressure as in vertebrates (the latter requires more flexible vessel walls). However, xylem pipes are also approximately cylindrical and this cost is still approximately proportional to the volume of the pipe.

With these ideals borne in mind, it can be concluded that Murray's law is also applicable to the xylem system of plants, although many plants do not reach this ideal of minimal energy expenditure due to physical restrictions, as we shall see.

Furcation Ratio

Blood vessels in animals typically bifurcate or branch into smaller vessels, but may also give rise to many branches. We can see that the furcation (forking) ratio is greater than or equal to 2. Things are not so simple in plants. Since flow can also travel sideways between vessels in the xylem systems of plants, more arrangements are possible, as shown in the diagram below:

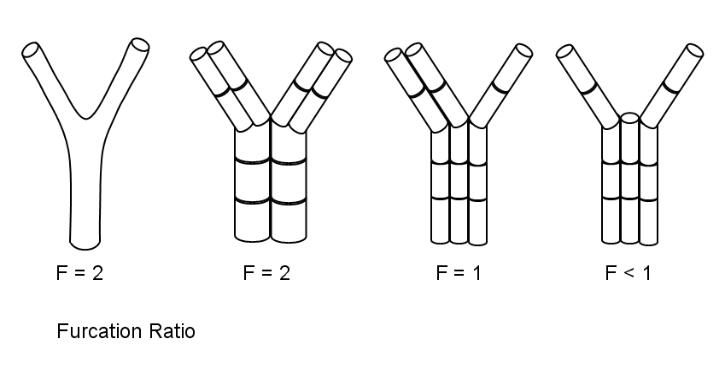
In this diagram, a typical bifurcating blood vessel of an animal is shown on the left. Three different arrangements in plant xylem are illustrated. This is not exhaustive, all we can see about the xylem system is that F is greater than zero (F > 0).

Let us put all this together on a couple of graphs and see what we get!

The first of these graphs shows leaf specific conductance (LSC) as a function of 'conduit taper'. (Based on data in: McCulloh and sperry, 2005). To remind the reader this is the hydraulic conductivity of a stem or branch divided by the total surface area of leaves supplied by that stem or branch. In this case, conductivity has been defined as flux (the flow rate of water in kg/s) divided by the pressure gradient driving that flow (in Pa/m). The conduit taper is a measure of how successful branches of the vascular system conduits narrow: it is the ratio of diameters of the daughter branch to the parent branch.

Why trees and vines have different woods

The above graph shows the relationship for LSC as a function of conduit taper when the ideal of Murray's law holds (solid line). It also shows the relationship for three different furcation ratios (F). Compound leaves of trees and shrubs (with high F) follow the Murray's law ideal. Vines can also approximate this ideal. Trees, however, can only approach this ideal with F = 1 and a conduit taper close to 1.0. Note that to achieve this ideal, trees have had to settle for a lower LSC (conductivity/leaf area) which is a result of having a low F. The apparent reason for this is that the xylem conduits of tree stems and woody branches also function to provide support and mechanical strength. This forces trees to adopt a hydraulic architecture which optimizes, or at least compromises, the need for support. To remain stable the total cross-sectional area (proportional to the sum of r-squared) of a tree at each branch level must either reduce or remain constant, otherwise the tree would be top-heavy like an inverted cone. This line of mechanical stability is indicated by the dashed line. Trees must stay below this line and so can only approach Murray's law by having a low F and a low LSC.

Vines rely on other plants for support and so their xylem conduits are less important for support and so can move above the line of stability to approach Murray's law. They do this by having very large xylem vessel diameters in the main stem, which can conduct rapidly and result in a higher F. Larger vessels, however, give xylem tissue a lower density of wall material and it is this wall material that provides the bulk of the mechanical support. This means that trees need to have narrow xylem conduits. Compound leaves have different mechanical requirements (taken over by parenchyma, collenchyma and sclerenchyma) and so their xylem vessels are freed of mechanical constraints and can be high conducting.

The graph below shows a different way of presenting this kind of data. This shows the deviation from Murray's law as a function of F, by plotting the ratio of total radii cubed for each order of branching relative to the parent branch on the vertical axis. For example, we could consider the radii cubed of the main boughs divided by the radius-cubed of the trunk. This graph is based on data in: McCulloh et al. (2004).

Why conifers and hardwoods have different woods - the importance of conduit diameter

The pressure needed to lift water from the ground to the top of a tree must overcome the weight of the water column, that is it must exceed the hydrostatic pressure. It must also overcome the resistance due to friction (viscosity) between the fluid and the side-walls of the conduit. Since only those xylem vessels formed by vessel elements are called vessels, in the strict sense, the term 'conduit' applies to both 'vessels' and pipes formed by tracheids.

This gives a minimum pressure of about 3 MPa needed for transpiration to draw sap up the xylem to the top of the tallest tree. This is about the safety limit, since at this pressure water begins to cavitate due to fracture of the water column subjected to such high tensions. The tensile strength of a water column depends on impurities and perhaps other factors and is not well predicted by theory. Tensile strength is the ability of a substance to resist stretching without breaking. A water column being pulled up a tree by negative suction pressures that result from evaporation and transpiration of water from the canopy against its own weight and against friction is under tension and will snap if the tensile forces become too high. Air will fill the vacuum that would otherwise result and the conduit is cavitated. Cavitation happens for a number of reasons, but results in air bubbles forming inside the conduit which may block xylem sap flow. This is perhaps the main factor limiting the height of the tallest trees.

The speed of flow in the xylem can be estimated using the Hagen-Poiseuille law. This is for non-turbulent flow which is certainly the case in xylem where we have creeping flow.

The tensile strength of a water column decreases rapidly below about 5^oC and breaking of the water column could be a cause of cavitation in taller trees, perhaps in Sequoia, for example, which is at around the maximum predicted height to pull a water column up the stem by suction (which subjects the water to tension). Such suction (due to transpiration) must overcome both the weight of the water column and the friction between the water and the vessel walls. Even in much shorter plants, however, suction pressures can become critically high when plant tissues dehydrate and this may fracture the water column resulting in cavitation.

Conifers, such as pine trees (Pinus) have xylem conduits composed of narrow tracheids. This gives good
mechanical support at the expense of high hydraulic conductivity. This would lower maximum growth rates, but
these trees compensate in part by being evergreen to lengthen the growing season. Narrower conduits are also
less prone to cavitating (becoming blocked by air) under cold conditions so conifers compete well in cold climes. Or at least this has been claimed, however the reality is more complex as we explain below.

Above: tracheary elements (cells that make up the xylem conduits); left: vessel elements or vessel members, found in many dicotyledons including broadleaf trees, are made up of cells called vessel members that have lost their living protoplasts, and so form hollow tubes, and stack end-to-end to form a vessel. Each vessel element typically has a perforation plate at each end, containing one or several large pores to allow xylem sap to flow from one element to the other uninterrupted. In ring-porous trees with wide diameter vessels, a single vessel may extend almost the whole length of the tree, but many extend a few meters before connecting to another vessel perhaps via a perforation plate in a side wall. In any case, adjacent vessels are connected by groups of smaller pores, each in a thinner area of the cell wall called a pit. The pits are arranged in aligned pairs, one pit on each vessel member in adjacent vessels forming a pit pair which allows xylem sap to be exchanged between the vessels.

Above right: a tracheid, as found in conifers, which also loses its protoplast to form a hollow structure but of much narrower diameter; these are typically connected to other tracheids but only via pit-pairs and not via wide perforation plates, often through their overlapping ends and side-walls, allow xylem sap to flow from tracheid to tracheid in a zig-zag fashion. The pits are typically abundant on the overlapping ends of tracheids for this purpose and are often in a single row. Hence, the conduits formed by tracheids are not considered as true vessels. In both types of tracheary elements, pits may also occur between the element and adjacent parenchyma cells.

Data obtained from the Yew, Taxus baccata (Cochard et al., 2006: doi/10.1111/j.1469-8137.2006.01947.x) demonstrate that cavitation is much more likely at higher temperatures, as long as the water does not freeze. This agrees with the experience of engineers that water is more likely to cavitate in a pipe at high temperatures. This happens when the pressure in the pipe drops below about the vapor pressure, which means that the water can not exert enough pressure to oppose the growth of air bubbles. This happens, for example, when the flow is disturbed by a sudden change in flow rate or if the pipe is suddenly bent, as might happen in a plant when wind bends a stem, causing local regions of low pressure.

However, cold has an additional effect if the water freezes. Freezing and subsequent thawing of xylem in extreme cold is a major trigger of cavitation. Extreme cold can also dehydrate plant tissues, resulting in critically high suction pressures that may fracture the water column. 

When water in the xylem is stationary, its pressure is static and hydrostatic, i.e. due to the molecular vibrations of water molecules (static pressure) and the weight of the water (hydrostatic pressure), and when suction is applied the pressure will drop and become increasingly negative as the water starts to move. This would be expected to increase the risk of cavitation, as could interrupting flow by bending of a stem or branch in the wind. Cavitation is a complex phenomenon and incompletely understood.

Engineers have also found that cavitation is less likely to occur in pipes of larger diameter. However, the flow, possibly turbulent, of water in a large copper pipe is not quite the same as the creeping flow of water in the xylem. Furthermore, it may depend whether the fluid is being moved by positive pressure or by suction (negative pressure). Creeping flow is flow which is dominated by viscosity and has a Re (Reynold's number) less than 1. Cavitation in creeping flow is thought to originate mainly from contaminant particles, such as dust, as is also the case in rapid flow. When a flowing fluid moves over the surface of a solid particle, regions of low pressure form next to parts of the particles surface and this can trigger air-bubble formation and cavitation. In plant xylem conduits, high suction pressures and freeze-thawing are generally thought to be the main cause of cavitation.

High-suction pressures occur under two circumstances. One, when the tree is nearing the maximum possible height. A simple calculation suggests that the maximum theoretical height for a tree is around 150 m (depending on conduit diameter and hence resistance to flow due to friction) beyond that and the suction needed to overcome gravity nears the maximum tensile stress for water and the water columns begin to fracture and cavitate. Redwoods are at about this maximum height. Secondly, even in a much shorter plant suction pressures can become high enough to fracture the water columns when water is scarce such as in times of drought. Continued evaporation of water from the leaves will increase suction pressure. This is a potential danger to smaller plants too, not just trees. Increasing suction pressures must be generated to remove water from the drying soil.

Freeze-thawing causes cavitation because gases are less soluble in ice than in liquid water, so when water freezes bubbles form. When the conduit thaws, these bubbles will either return to solution or merge or otherwise expand to block the conduit.

Experiments have shown that cavitation in wood occurs more easily in wider conduits when the water column is subjected to tension. Thinking in terms of stress-strain curves it is not clear why this is the case since the tensile strength should be independent of diameter of the water column. Perhaps the measured strength of water columns in narrower conduits is increased by boundary or 'wall effects' or the adhesion of water to the sides of the vessel. However, data are not clear and in some plants no clear correlation exists between conduit diameter and the likelihood of cavitation. A further complication is that tests are carried out on bulk tissue rather than individual conduits and in plants there are lateral pores connecting the flows in adjacent conduits together. This means that when one conduit cavitates it may trigger cavitation in adjacent conduits as air diffuses across these lateral pores. By the same token, however, water can flow sideways to a new vessel to circumvent a blockage. Plants have mechanisms to reduce this risk and to isolate a cavitated conduit but the efficacy of these mechanisms depends on species and adds another factor affecting cavitation. (I also wonder to what extent these side-connections invalidate the use of Poiseuiille's equation for pipe flow since we are now dealing with both series and parallel resistances).

Some plants are known to divide their xylem into functionally separate sectors, each sector supplying part of the canopy. If cavitation spreads through lateral pores from a cavitated vessel, it will at most block only one sector, depriving part but not all of the canopy of xylem sap. Such stem sectoring produces what we call dissected wood and is found in some plants adapted to dry conditions. The downside is that xylem sap has a less interconnected network to ensure all parts of the canopy are supplied when there is a blockage, but at least the blockage is contained so only part of the plant is affected.

One plausible explanation for why larger vessels are more prone to cavitation when under tension in creeping flow relates to the surface tension in bubbles produced by say a freeze-thaw cycle. Larger bubbles, sitting in a wider vessel, have a larger radius of curvature and hence less surface tension, which means that gas pressure inside the bubble can more easily cause its expansion and the bubble is more likely to take more gas out of solution and expand to block the conduit when suction is applied. Smaller bubbles sitting in a narrow tracheid have a smaller radius of curvature and higher surface tension, meaning that the bubble is more likely to contract and dissolve the gases back into solution, unblocking the vessel.

Large diameter vessels enable a higher transpiration stream velocity for a given suction pressure, due to reduced friction between the xylem sap and the conduit walls. In principle we might expect this to enable trees with wide vessels to reach greater heights, but the tallest trees are conifers with narrow conduits made up of tracheids. (The term 'vessel' is, unhelpfully, restricted to the broader conduits of broadleaf trees and consist of cells called vessel elements, though broadleaf trees may also have narrow tracheids). Broadleaf trees instead use their wide vessels to increase flow rates to transport more water to the leaves, maintaining high suction pressures. Deciduous trees, with their wider conduits, transpire water about ten times faster than conifers, measured per unit of leaf dry mass. This allows them to obtain more carbon dioxide for photosynthesis and minerals for growth. Thus, we would expect broadleaf trees to be faster growing, however, they can not maintain high transpiration rates in winter when the ground is frozen and the heat to drive transpiration by evaporation lacking and so are generally deciduous, shedding their leaves in winter.

Nevertheless, in both conifers and broadleaf trees, the average diameter of conduits increases as path-length (plant height or length) increases, helping to reduce the friction and hence the amount of suction pressure required and thus to minimize the increased risks of cavitation in tall plants. There are now two choices: lots of narrow vessels running from root to leaf without furcating, or wider vessels at the stem base that furcate into narrower vessels in the leaves. The latter is the adopted strategy: as plants become taller they tend to increase the diameter of conduits at the stem base to reduce friction and resistance to flow, helping to offset the increased pressure gradient needed to transport water a greater distance. This partially reduces the increased risk of cavitation in tall plants, whether they are self-supporting trees or long vines or lianas.

Conifers also rank among the fastest growing trees, however, despite their lower rate of water transport, in part because they are evergreen and continue growth in winter, but this can not be the whole story. Conifers must possess additional adaptations to maintain growth at low transpiration rates. Nevertheless, deciduous trees begin to lose their transport advantage in cold climates where conifers, with narrow tracheid-based conduits dominate.

Summary. Wide conduits allow a faster transport rate. This reduces the pressure needed for transport and so can reduce cavitation risk since the major cause of cavitation in trees appears to be fracture of the water column under tension, at least in the tallest trees and during times of drought or periodic freezing. Conversely, however, narrower conduits may sometimes have a reduced cavitation risk, at least in some species, though the reasons for this are not entirely clear. These trade-offs presumably help explain the variation in conduit diameter in different species living in different climates and in plants of differing height, leading to a variety of vascular architectures found in nature. More research is needed both from the perspective of fundamental fluid mechanics and plant physiology to better understand these systems.

Caveat: available data is still scanty and more studies need to be done to compare hydraulic conductivity in different woody plants growing in different conditions. However, what data is available supports the following conclusion.

Hardwood trees have larger xylem vessels which can conduct sap at a higher rate, especially those with ring- porous woods (such as Ash). These trees also have a higher furcation ratio (F) in their woody parts (though still lower than in vines and compound leaves) since the vessels in the main stem are especially wide. The reason for this is that conductivity remains high throughout the main stem so that topmost branches are not deprived by lower branches. Also, as we have seen, wider basal vessels reduces the resistance to flow and hence the pressure needed to cause sap ascent which reduces the risk of cavitation.

Taller trees and longer vines tend to have wider vessels in the basal parts of their stems - the xylem conduit diameter increases from apex to base. This reduces resistance to flow in longer stems, hence reducing the need for high tensions to drive flow. In other words, with wider conduits the water can be drawn up with less pressure and hence reaches a higher flow rate at a lower pressure according to Poiseuille's equation. However, it may reach a maximum diameter at some point along the stem and then the diameter will maintain this constant maximum further towards the base. This maximum may reflect some growth limit on individual conduits or may be a compromise since wider conduits have an increased risk of cavitation from drought or freeze-thaw events once air bubbles are present.

These trees can afford to do this because they have more sclerenchyma fibers in their woods. In conifers about 90% of xylem tissue consists of conduits, in ring-porous hardwoods this is as low as 10% (and diffuse-porous woods are intermediate at about 25%). This means that the xylem vessels can sacrifice mechanical strength and have larger diameters and higher conductivity since other tissues now take on the main supportive role (division of labor).

Ring-porous and Diffuse-porous Woods

Hardwood can be divided into two main types: ring-porous and diffuse-porous.

Above: In cross-section hardwood can be seen to contain many pores, each pore being either a single xylem vessel in cross-section or a group of adjacent xylem vessels (connected by pit-pairs). Ring-porous wood is a specialization found almost exclusively in northern temperate trees. Early in spring vessels with very large diameters form in the early wood, followed by smaller vessels in later wood, making the annual growth rings easy to see. In diffuse-porous wood the vessels tend to have more-or-less the same smaller diameter throughout a growth ring though there may be a band of late wood with small vessels and annual growth rings are often still apparent. Intermediate patterns occur in some species. Ring-porous wood is an adaptation to resume rapid growth at the start of the season when trees must compete for the spring light. Parenchyma cells in the wood may pump stored sugars into the early xylem vessels (presumably via the connecting pit-pairs) to fuel rapid bud expansion and in some species parencyhma cells can be seen making direct contact with xylem vessels as contact cells. Apart from this axial parenchyma, arranged in vertical columns in the wood, there are the radial plates of parenchyma cells called rays and wood also contain narrow thick-walled cells (with or without living contents) that join end-to-end to form structural fibers to give the wood strength. Hardwoods may also contain tracheids in addition to vessels.

See also: https://www.wood-database.com/wood-articles/hardwood-anatomy/

How do Trees Recover Xylem Function after Cavitation

Since cavitation occurs when the pressure driving the flow drops below the vapor pressure, a plant can drive air back into solution by generating high positive pressure in the xylem. Different species use different mechanisms and some have no special ability to recover from cavitation at all, but may rely entirely on growth of new xylem. Trees grow wider each year as a new layer of xylem is deposited each growing season. This gives rise to the familiar tree rings.

For example, a diagrammed sector of a two-year old woody stem is illustrated below. Some of the embolised vessels have recovered but not all, but the total fraction of embolised vessels is reduced by growth of new wood:

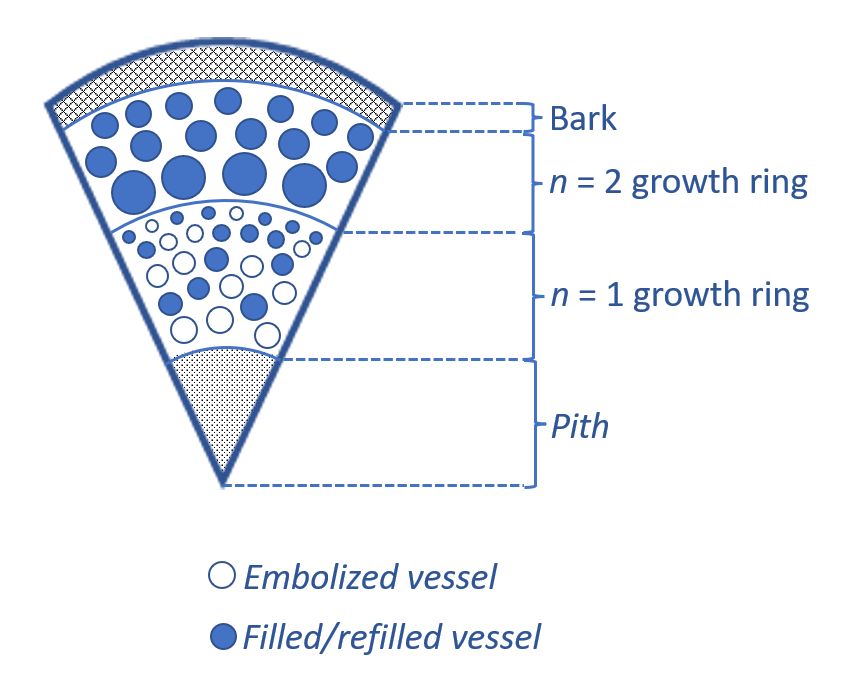
Roots can generate positive root pressure, in particular because they expand metabolic energy to drive mineral nutrients into the roots from the soil, which pumps in water by osmosis. In some trees, the stems can also generate positive xylem pressure, or stem pressure. This seems to be due to axial parenchyma, parenchyma in the wood that forms vertical columns parallel to the xylem conduits. These parenchyma can actively pump solutes, such as sugars, into the xylem sap, causing water to follow by osmosis and generating positive pressure.

Finally, as discussed in other articles in the structure of wood plants have safety mechanisms to reduce the risk of cavitation in the first place. Apart from the more obvious measures to reduce the excessive dehydration that generates high suction pressures, such as closure of stomata and drooping of leaves, plants may seal off cavitated conduits that fail to recover to prevent the air spreading to other conduits and seeding further cavitation. In the tracheids of conifers special pit membrane valves can immediately seal off a cavitated tracheid in a reversible fashion. Other trees may secrete tyloses or gums to more permanently seal off cavitated conduits.

Generally, trees adapted to dry conditions have more obvious adaptations to prevent and/or recover from cavitation.

Conclusion

It is remarkable that detailed studies of hydraulic architecture have shed so much light on the perplexing problem of the functional benefits of different wood types. I have previously pondered this problem to no avail.

Plant hydraulic architecture is an example of one area of biology that has benefited from multidisciplinary analysis. Biological systems are often too complex for mathematical and physical analysis, but increasingly the use of these tools is bearing results. There is still an incomplete understanding of the basic principles of fluid flow in a xylem-like system (parallel bundles of narrow tubes with creeping flow driven by negative pressure) and the risk of cavitation. This calls for more basic fluid mechanics investigations.

Differences between species in terms of conduit diameter, velocity of flow, cavitation risk and ability to repair a cavitated system require further study though a picture is beginning to emerge.

References

Brodersen, C.R. and A.J. McElrone. 2013. Maintenance of xylem network transport capacity: a review of embolism repair in vascular plants. Frontiers in Plant Science 4:108.

Cochard,H., T. Barigah, E. Herbert and F. Caupin, 2006. Cavitation in plants at low temperature: is sap transport limited by the tensile strength of water as expected from Briggs’ Z-tube experiment? New Phytologist 173(3): 571-575. https://doi.org/10.1111/j.1469-8137.2006.01947.x

Cruiziat, P., H. Cochard and T. Ameglio, 2002. Hydraulic architecture of trees: main concepts and results. Annals of Forest Science 59: 723-752. DOI: 10.1051/forest:2002060

McCulloh, K.A. and J.S. Perry, 2005. patterns in hydraulic architecture and their implications for transport efficiency. Tree Physiology 25: 257-267.

McCulloh, K.A., J.S. Sperry and F.R. Adler, 2004. Murray's law and the hydraulic vs mechanical functioning of wood. Functional Ecology 18: 931-938.

Transport in plants


Article updated: 27/2/15, 4/8/2018