Above: A simulation of a tree on a high-gravity world (carried out using TomTree (using v 1 but a more recent version is here: http://f-lohmueller.de/pov_tut/plants/plants_400e.htm) and Pov-Ray). The shape is not predicted to be very different from that on Earth, but the trunk and branches are significantly shorter.

Tree Equations and Alien Plants

What physical laws govern the structure, shape and form of trees? Can we construct a mathematical model and use it to predict the nature of alien trees growing on other planets?

In this section we look at some key equations describing plant/tree form and function and consider what the implications are for alien life. The first part of our analysis builds on that by Karl J. Niklas in his book (and research papers) on Plant Biomechanics.

We will examine the following 'tree equations':

Equation 1. Euler's column formula for a self-loaded column to model the support function of the trunk.

Equation 2. The beam equation for the self-loading of a branch as a cantilever.

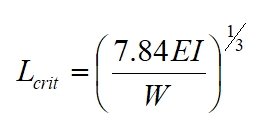
Equation 3. The transpiration equation.

Equation 4: The transport equation.

Equation 5. The growth equation.

Equation 6. The diffusion equation.

Of course these six equations can not model every aspect of tree biology, but they go a long way to explaining plant form and function.

We shall begin with Euler's column equation for an ideal column (an ideal column is one that is straight, homogeneous and free from initial stress. This equation allows us to determine the critical load (P), or conversely the maximum critical height (h) before a column permanently warps under its won weight - it assumes only self-loading and so only looks at (vertical) compression stresses, and ignores, for example, wind forces which cause lateral (sideways) forces to act on the column too. The elastic modulus is a measure of the stiffness of the material making up the column, but the overall stiffness of the column also depends upon the geometry of the column, which is included in the moment of area, I. In other words, we can estimate the maximum height of a tree before it collapses under its own weight.

Equation 1. Application of Euler's Column Formula

In this section we shall model a tree as a column, hollow or solid and potentially circular or elliptical in cross-section.

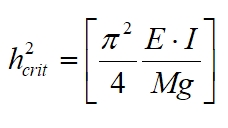
Where h_crit is the maximum height of the column before it warps under its own weight, E is the elastic (Young's) modulus (a measure of the stiffness of the material making up the column) and I is the second moment of area. We are considering a self-loaded column subject to its own weight (W = Mg) and so the load is mass (M) times acceleration due to gravity (g). The crown accounts for 17 to 44% of the above ground mass of a typical tree (about 32% of the dry weight) so the stem accounts for the bulk of the mass so neglecting the crown mass is a reasonable first approximation. The product EI is the flexural rigidity, a measure of the column's stiffness.

For a column of circular cross-section, i.e. a cylinder, we have:

Where: R_o is the outer radius and R_i the internal or inner radius of the stem; for a solid trunk R_i = 0. This gives us a measure of the distribution of material around the central vertical axis of the column: the more widely distributed the material is the more resistant the column is to bending, however, in practice we do not want the wall to become too thin as it may buckle especially when subjected to a sudden impact or twisting motion.

Now, using density = mass/volume we can replace M, the mass of the trunk, with density x volume, using:

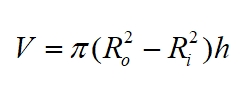
For a cylindrical trunk (volume = cross-sectional area x height). Thus we have:

Where: ρ is the density of the trunk (density of living wood). Note that the coefficient π²/16 ≈ 0.61685. Values for E and ρ vary from tree to tree, but typical values for an oak would be ρ = 720 kg m^-3 and E = 9.3 x 10⁹ Pa (but takes on a range of possible values, 11 x 10⁹ Pa is another acceptable value). Some 'typical' values for different woods are shown in the table below.

Tree	Density (kg m-3)	Elastic modulus (x 109 Pa)
Maple	650	11.0
Oak	720	9.3
Balsa	100	3.7
Cedar	470	4.4
Pine	600	8.8
Redwood	450	6.6
Ebony	1090	17.0
Larch	500	12.9
Bamboo	350	18.0

Note: the density value for Balsa is a low-end value to illustrate the full range of densities. Other sources give values of 170 or over 300 kg m^-3 with density increasing towards the base of the tree and towards the outside of the trunk.

For a trunk of density 720 kg m^-3, outer radius 0.5 m and inner radius 0.4 m we get the following trend for critical (i.e. maximum) height versus elastic modulus:

This gives us a maximum height of about 70 m for a trunk made of oak wood. Remember, this model only factors in self-loading due to the tree trunk's own mass. For a trunk of radius 0.5 m, but of solid construction the trend is the same but maximum heights are decreased slightly:

Despite having stronger stems, trees with solid trunks have more weight to support and this more than counters the gains in absolute strength. remember, this factors in static or self-loading only.

Safety factors

For the tree with the solid stem, our oak has a predicted maximum stable height of about 110 m, which compares to the maximum observed height of about 40 m. Real trees are much stronger than they need to be in order to support their own weight, since they have to support additional forces such as dynamic stresses due to high winds. in fact trees typically have a safety factor of about 4 or more. With a safety factor of 4, the 110 m maximum height equates to an actual maximum height of 27.5 m. A solid trunk of radius 0.6 m gives us a maximum height of between 150 and 160 m, sufficient for the maximum height of 40 m with a safety factor of 4. Real tree trunks are also not exactly cylindrical but tend to taper in an approximately conical fashion. They often have spreading buttressed bases and narrow apexes. This reduces the overall weight of the trunk, and lowers the height of the center of mass, increasing stability further.

If we think of the maximum potential height of a tree, say 130 to 150 m for a Redwood and take the density and elastic modulus as given for a Redwood in the table above, then we find that a trunk radius of about 1.1 m is sufficient to obtain this height with a safety factor of 4. Clearly Redwoods often have much wider trunk diameters than this at the base. Does this mean they have a higher safety factor than 4? a safety factor of 4 means that a wood-cutter must remove at least 3/4 of the wood from a cross-section of the trunk before a tree begins to collapse under its own weight (assuming negligible winds). Trees have to cope with the unexpected, such as high winds, frost damage, grazing and lightning damage; trees are built to last!

Hollow versus Solid Stems and Stem Geometry

If we think of a mature tree growing tall and straight in a competitive forest stand, it will grow mainly in height first, so young trees tend to be tall and slim and statistically these trees are the most prone to windfall. Over time, however, the trunk continues to thicken and at some point a breach in the wall of the trunk may allow fungi to access the dead heartwood and gradually bring about its decay. This actually improves the ability of the tree to support itself against its own weight, since its weight is reduced. However, resistance to dynamic loading (such as wind tending to bend the stem) will be slightly reduced due to a reduction in flexural stiffness (due to a decrease in the second moment of inertia). This can be offset to a large extent by having a wider stem. A hollow trunk will always have a lower flexural rigidity than a solid trunk of the same width. A hollow stem containing the same amount of material as a solid stem, and of the same height, will be wider and will have a higher flexural stiffness - the material is being used more efficiently. However, a thinner wall is also at increased risk of being breached should it be damaged.

Breaches in the trunk wall, due to damage or loss of branches followed by fungi gaining excess to the exposed heartwood, or indeed by fungal infection of the living sapwood, weaken the support provided by the outer shell. Other agents that may reduce the height of a tree include over-development of the crown as may occur when a pollard is then left to regenerate of its own accord. Pollarding involves removing the top of a tree whilst keeping new growth above the height of grazing animals such as deer. The tree responds by activating dormant buds and putting out a greater number of new shoots. This new wood may then be removed a few years later as a source of timber (e.g. for fencing) but if left to continue growth the tree may end up with an excessively heavy crown and branches may tear free, demolishing part of the trunk as they do so.

Giant redwood trees (using 'redwood' in the loose sense here to refer to Sequoia and Sequoiadendron) often suffer height loss through lightning and fire. Being tall clearly poses other risks. The heartwood of Redwoods is particularly resistant to decay and fungal attack, increasing their ability to resist dynamic stresses such as high winds. for such tall trees, the dynamic stresses exerted lower down the trunk would be enormous (though natural tapering of the trunk reduces this). In the absence of such dynamic forces, however, having solid stems reduces their critical height due to increased self-loading.

Similarly, in the animal kingdom, elephants (and formerly sauropods) have solid leg bones and straight column-like legs designed chiefly for supporting their weight. In elephants these bones are solid, whereas in most animals the limb bones are hollow. This has been explained by stating that the solid leg bones of the elephant support its weight better, that is they are solid for static loading, and these animals are sometimes called 'graviportal'. Having straight limbs minimizes dynamic loading when standing still, however, when elephants run the dynamic loads on their limb bones must be tremendous due to the sheer strength of their muscles. The solid bones of the elephant increase resistance to dynamic loads and elephants are indeed quite fast runners. The fastest animals, however, are those with a body mass around 100 kg and these have hollow bones, which reduces weight whilst maintaining flexural rigidity if the bones are wide enough. This economizes on amount of material: the bones of these 'cursorial' animals optimize flexural rigidity for a given mass of bone. Presumably elephants would need unfeasibly wide limbs and the hollow walls of such bones may be prone to buckling in such heavy animals (in the way an aluminium drinks can will easily buckle is stressed in certain ways). Thus elephants and sauropods are simply at the mass limit and it is not possible to economize on the amount of bone by having wider hollow limbs. It should be understood that if tree trunks and bones were subjected only to the static stresses of self-loading then they would be very thin and narrow to reduce their own weight! Additionally, the limbs of the elephant must support the additional and considerable bulk of the rest of its body (discussed below).

In both leg bones and tree trunks, the greater forces are dynamic bending and twisting forces, not forces due to self-loading. Muscles typically work against unfavourable leverage and subject bones to tremendous bending stresses in order to move them (as can be shown by calculation). Trees are similar more stressed by bending forces in high winds than they are by their own weight.

Trees grow by depositing new wood on the outside and must do this every year as older wood becomes non-functional. Thus, a tree must keep increasing in width which requires an increasing volume of wood. Eventually, the leafy crown may not produce sufficient food to support the growth of a complete shell of new wood (and phloem) and gaps may open in the trunk shell where new growth is absent and dead material decays, so the trunk is not only hollow but open. Mechanical damage can also breach the thin wall of a hollow trunk. Branches may subsequently die if they do not receive sufficient sap. In oaks this results in a 'stag's-head' appearance where old dead branches stick out like antlers, a condition that may be brought on earlier by periods of drought. Although this loss of sapwood may reduce the amount of crown that can be supported, it may reduce stresses due to wind, as the wind may pass through the trunk, so such trees are generally not prone to windfall, but due to gaps in the shell-like trunk they are more prone to suffer partial collapse. Decayed deadwood is not necessarily wasted, however, since as the deadwood decays trees may put down (adventitious) roots into the hollows in the center of their trunks to absorb nutrients released by fungal action and so can recycle nutrients into the growth of new wood in the outer trunk. Hollowness is thus largely inevitable, but also exploited to prolong longevity.

Nevertheless, ancient hollow trees are reportedly less frequently toppled by wind than younger more slender and more solid trees. Trunk width is clearly of major importance since this increases flexural rigidity, though the tallest trees also maximize the total cross-sectional area of their trunks, analogous to the leg bones of the elephant. An additional factor to consider are additional static loads supported by the column. So far we are saying that if a column supports only its own weight then it needs to be as light as possible and can then climb to an arbitrary height, but when subjected to bending forces it needs to be wide and being hollow can economize on material as well as reduce static loading. A third situation is when a column bears a static load in additional to its own weight: a column supporting a roof might be an example of this. Clearly such a column requires a certain thickness to resist compression by the external load. In the case of a tree, the trunk accounts for the bulk of the above ground mass and so Euler's column formula for a free-standing column is a reasonable approximation. In the case of elephants and sauropods their column-like legs must support the huge bulk of their digestive tracts and such large guts are useful for digesting the toughest of plant materials. Thus, the legs of sauropods and elephants function rather like the columns of a temple.

It is possible to further economize on material by changing the cross-sectional shape of the column (or beam). A column (or beam) of elliptical cross-section is stiffer when bent in the direction of its widest axis, so if a structure is stressed preferentially in the same direction then this geometry will be a more efficient use of material. Bones may achieve similar effects by developing wings of bone for muscle attachment. (Though it should be borne in mind that in life fibrous cartilage forms the attachment site of tendons and this may or may not ossify with time and use so an analysis of bone by itself may be misleading).

Many trees have elliptical stems and branches. This is because the tree responds to the stresses acting upon it as it grows. In an ellipse one radius (the major radius) is larger than the other (minor) radius and in these plant parts the long axis will be aligned with the direction that experiences greatest bending stresses - increasing moment of area and stiffness whilst economizing on the total mass of material used.

Trees on Planets with non Earth-like Gravity

Next, we make this critical height a function of gravity. On Earth the force due to gravity is about 10 Newtons (9.8 N). How tall might trees grow on planets with more or less gravity than this?trend below shows our prediction of how gravity might effect the maximum height of trees:

The data in the graph above are for solid cylindrical stems of 2.0 m diameter, E = 1 x 10¹⁰ pa and r = 720 kg m^-3. The heights shone are critical height / 4, that is assuming a safety factor (SF) of 4.

Remember that trees strive to be tall in order to compete for sunlight, however, there are limits, and from this result we might expect trees to be shorter on a higher gravity planet, but not by that much - even when the gravitational force is 40 N (4 times stronger than on Earth) the predicted height of trees is only reduced by about half (the critical height is divided by the cube-root of 40). Planets with much higher gravity than this are unlikely to have a conventional solid surface as they will hold on to a very dense atmosphere and become gas giants, unless they lose that atmosphere catastrophically. On such planets the best potential place for life is in the atmosphere.

Wood Density

Additionally, a tree could overcome this if it had less dense tissues. The effects of density on critical height (divided by 4 to account for a safety factor of 4) are shown below:

The data in the graph above are for solid cylindrical stems of 2.0 m diameter and E = 1 x 10¹⁰ Pa. The heights shone are critical height / 4, that is assuming a safety factor (SF) of 4.

Clearly low density wood can, according to our theory, support a taller tree by reducing self-loading. certainly coniferous softwoods tend to reach greater heights and have wood densities around 450 to 600 kg m^-3. However,a hardwood like an oak has a wood density of around 720 kg m^-3 and typically attains heights of over 30 m. It should be remembered that wood functions to transport sap from the roots to the rest of the tree as well as for support and hardwood is designed to maximize the rate of sap ascent in early spring, perhaps at the expense of  maximum tree height: height is not everything. In any case the Balsa (Ochroma pyramidale) normally grows to about 30 m in height only, however, it grows very rapidly as it can produce its low density wood quickly, reaching just short of 30 m within about 10 years. The base of a Balsa tree is often greatly buttressed. Balsa trees are short-lived, however, with typical lifespans of 30 to 40 years. Older trees may have hard outer layers of wood and hollow stems with a diameter of 2 m or more. This rapid growth strategy allows the Balsa to quickly fill gaps in the tree canopy ahead of competition: Balsa is a pioneer species. Very low density wood is of course prone to mechanical injury and not so suitable for a long-lived species. The hard wood on the outside of older balsa trees compensates for loss of the heartwood.

A tree like balsa has a density as low as 380 kg m^-3, or occasionally as low as 100 according to some sources (this depends on location within the trunk and age as already explained) a redwood 450 kg m^-3, whilst an ebony might have a density as high as 1120 kg m^-3. Now redwoods can reach heights of over 115 m. This discrepancy can be explained partly by the great diameter of redwood stems and partly by the fact that redwood trunks strongly taper. Indeed all tree trunks taper to a greater or lesser degree. A tapered stem reaches the same height by using less material (lower mass) and also distributes stresses evenly throughout the column (in a cylindrical column, the stresses are greatest at the base, remember that stress is force per unit area in this case). For a tapered trunk, the critical height increases. For a trunk in which the topmost radius is half the basal radius (a truncated cone) the critical height increases by 26%, whilst a greater taper may increase it by up to about a third or more.

In conclusion, we see that the mechanics of tree trunks 9and animal limbs) are rather complex and so we should beware over-simplistic analysis!

Equation 2 - The Beam Equation and Tree Branches

Tree branches can be modeled as cantilevered beams, similar to columns held at an angle, fixed at on end, and subject to the self-loading of their own weight per unit length. The equation for the critical length of such a beam, that is the maximum length before it warps under its own weight (and assuming it does not fail at its point of attachment with the trunk) is given by:

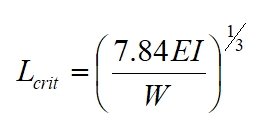
Where: E is elastic modulus, I is second moment of area and W is weight per unit length, which for a horizontal branch is given by:

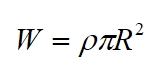
(For a branch angled at the vertical trigonometry can be used to find the weight acting in the vertical component). For a solid cylindrical branch of circular cross-section, the loading increases with branch radius (which increases branch mass per unit length but conversely increases flexural rigidity) iand the critical length n a manner proportional to R^2/3 as shown below:

The weight per unit length increases as R² but flexural rigidity increases as R⁴ so overall, critical length increases with branch thickness. Critical length decreases, however, for a branch of fixed radius as density increases:

The model above is for a cylindrical branch of radius 0.2 m. clearly, tapering of the branch will increase this critical length but the weight of side-branches and foliage will decrease it. Again we can assume a safety factor of about 4 and so divide this critical length by 4 to obtain a more realistic maximum. For an oak tree this gives us a maximum horizontal length of about 25 m.

On an alien world, as the strength of gravity increases the branches are predicted to shorten in proportion to the shortening of the stem, that is as g^-1/3, so that the overall tree shape is maintained.

Water Transport

So far we have only considered the effects of gravity on tree shape. Also of importance is the need for a tree to move water up the trunk from the soil, via the roots, into the leaves. The function of the leaves is to obtain sunlight and carbon dioxide for photosynthesis. To achieve this, the leaves must be thin and plate-like (otherwise too many non-photosynthesising cells would occupy the centre of the leaf where light cannot penetrate). They also need leaf pores (stomata) to let the carbon dioxide gas pass from the atmosphere into the leaf. A consequence of this is that water will also escape by evaporation from these pores (a process called transpiration) and this water must be replaced by water moving up the plant from the roots in what is called the transpiration stream. However, plants exploit the transpiration stream to carry mineral nutrients from the soil to the cells and transpiration also helps the sunbaked leaves to keep cool.

See also: Transport in plants

Equation 3 - The Transpiration equation for Stomatal Conductance

Using Fick's Law we can derive an equation to model diffusion across the stomata. Essentially, this is one-dimensional diffusion across stomata modeled as narrow tubes. However, the diameter of the tube is also important and a number of variants on this equation incorporate corrections to account for this. We use one such simple correction below. Note that the variants given of this equation all give values of conductance within an order of magnitude of one-another and the patterns and trends are essentially the same (all the ones I have seen differ only by a constant of proportionality).

Plants can open and close their stomata in response to a variety of internal and external conditions and also in accordance to an internal clock. In addition, in the long term, plants can vary both the number (density of stomata per square mm of leaf surface area) and the maximum size of the stomatal apertures. These characteristics differ greatly between species, but are also capable of some adaptive variation within a species. For example, it has been shown that as carbon dioxide levels have increased, both by natural means since the last peak glacial period of the Ice Age and more recently from anthropogenic emissions, plants respond by  reducing stomatal conductance. This is achieved by having fewer, larger pores per leaf, as explained below:

This effect is also reflected in our conductance equation, shown below, in which conductance, G, is not only a function of stomatal depth, d, and total leaf area accounted for by stomatal pores (stomatal density, n, multiplied by the mean pore area of the stomata, a) but also of stomatal radius, r. If the total pore area is kept constant, then stomatal conductance decreases as pore radius increases, as shown below:

Each species occupies a narrow part of such a conductance curve, with some species having intrinsically high conductance (those from carbon dioxide poor atmospheres in which water is plentiful) whilst some have lower conductance (those from carbon dioxide rich atmospheres, or regions of water shortage). The fact the increasing the levels of carbon dioxide causes plants to adapt by reducing conductance (whilst still possibly increasing net photosynthesis) reduces stomatal conductance, shows the importance of conserving water - stomata function primarily to allow carbon dioxide to diffuse into the leaf, and although the transpiration stream in the xylem transports some useful materials, like minerals from the roots, this function is secondary and xylem transport is in excess of that required for these transport functions, serving primarily to replenish water lost by the leaves through their stomata. However, i am not aware of any studies quantifying the importance of mineral transport - could plants without stomata obtain sufficient nutrients without flow in the xylem?

Within a species, maximum pore area and stomatal density typically vary by 2-fold in response to environmental conditions. Densities may vary from 100 to 1500 per square mm in different species, and maximum pore areas from 30 to 170 square micrometres.

Of course, if the stomata close, then both the pore radius and the total area of pores reduces and conductance naturally decreases, as shown below. Notice from the graph that the stomata affect the greatest relative changes on conductance at very small pore radius. Most stomata are between 3 and 15 micrometres (0.003 and 0.015 mm) in radius and so can rapidly regulate conductance by slight changes in diameter:

The graphs below show the shapes of curves of stomatal area as a function of stomatal density (now given the symbol x so as not to confuse Mathcad, x = n) different conductance values. See how at higher conductances the curve shifts up and to the right. Similar plots can be seen in many papers on plant physiology.

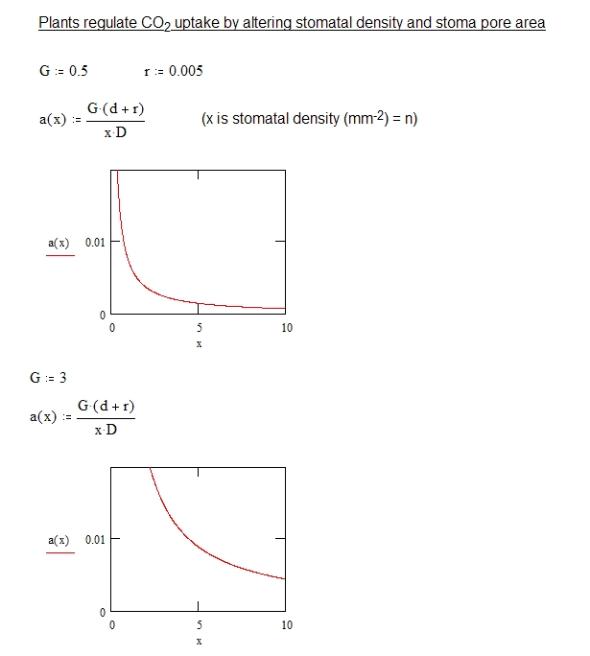
What about alien plants? We might expect those plants that live in a carbon dioxide rich atmosphere to have fewer larger pores for carbon dioxide absorption. Carbon dioxide may also, however, have major effects on tree branching patterns and leaf shape, as we shall explore qualitatively below (the diffusion equation).

Equation 4 - Transport Equation (Poiseuille's Law)

One very important equation for plant transport is the equation for water potential (see transport in plants). Here we look at the equation governing flow in xylem and phloem: Poiseuille's Equation for laminar, parabolic flow in a straight tube:

See transport in plants for a more detailed description of the physiology of sap transport in plants, a brief summary of which follows below.

This flow describes flow in xylem especially, but also bulk flow in phloem, quite accurately. However, in phloem, different forces give rise to the pressure gradient which drives the fluid flow. In xylem, the pressure gradient is a negative suction driven by evapotranspiration of water from the tree canopy. Evapotranspiration consists of evaporation through the cuticle of the leaves and also transpiration through the open pores or stomata of the leaves which take in carbon dioxide for photosynthesis. The need for carbon dioxide makes this water loss largely unavoidable and sets up a pressure gradient that sucks water up the stem through the xylem conduits. This stream of xylem sap is used by plants to carry mineral salts as nutrients from the roots to the aerial parts. There is also a small positive pressure contribution from the roots, called root pressure, which results from the active (energy-consuming) pumping of salts by root cells from the soil into the xylem. This pumping is necessary because of the relatively low soluble mineral content of soil and draws water after it by osmosis.

In phloem, generally positive pressures drive phloem sap through the phloem conduits from one part of the plant to another. Generally organic building-blocks and energy sources manufactured in the leaves and other green aerial parts are transported in the phloem to where they are needed, but phloem can flow in any direction up or down a plant. The transport of sugars into the phloem at sources and its removal at sinks drives water with it by osmosis and creates the pressure needed for bulk phloem flow.  Sources include photosynthesising leaves, storage organs which are mobilising their food reserves, e.g. bulbs in early spring, whilst sinks include growing plant parts, roots, heavily shaded leaves, growing storage organs (such as a bulb filling with food reserves before winter) and developing fruit. Flow in the phloem also has a pulsatile quality, which is thought to be due to the loading of sugars into the phloem at regular intervals by companion cells.

Note that the flow rate of sap is proportional to the square of vessel diameter. The cross-sections of xylem vessels varies considerably. Broad-leaved trees, like oak trees, produce wide-diameter vessels in new wood (early or Spring wood) deposited in Spring and narrower vessels in summer. The early vessels enable the rapid transport of xylem sap for rapid spring growth and to replace the water lost by evapotranspiration when the new foliage opens. However, late or summer wood has smaller diameter vessels, since the high pressures generated by evapotranspiration in the summer heat is more likely to cavitate larger diameter vessels. Cavitation occurs when the water column breaks and air fills the space, resulting in a bubble which is difficult to shift and which may block a vessel temporarily or even permanently. Cold
conditions also increase the likelihood of cavitation and so cold-hardy conifers have much narrower vessels (tracheids).

Each xylem vessel may be several centimetres to a meter or so in length at which point the sap moves across into another adjoining vessel, such that the xylem sap takes a somewhat zig-zag path up the stem. This is beneficial, since it allows sap to circumvent blockages or breaks due to wounds, etc. without depriving whole sectors of the crown.

In tiny plants, namely mosses, water moves up the plant by capillary action, whether it is moving up the outside of the stem or inside the stem in more-or-less specialised tissue. No other driving force is thought to be necessary to move water up a plant only a few millimetres or centimetres tall, though evaporation likely also contributes.

Equation 5 - The Growth Equation

A tree must invest a lot of resources in its stem, to maintain the dominant position of its leaves high in the canopy. The trunk of large trees is not photosynthetic at all and so these materials do not bring direct gain in terms of growth. The growth of a tree is driven by its leaves (supplemented by nutrients and water from the roots). The fastest growing plants are almost all leaf. Duckweed is one of the fastest growing of all plants, and each plant consists of a little leaf and a tiny root and the plant floats in the water. Single-celled algae (protoplants) are even faster growing. In contrast, a large tree which must invest so many materials in supporting structures is very slow growing relative to its size, that is in terms of percentage  weight or mass increase.

The growth equation is:

This gives us the growth rate, R, which is the rate of increase in mass relative to the present mass. This is relative growth (and obtained by logarithmic differentiation).

A young sapling grows more-or-less exponentially and relatively very fast. However, once a tree reaches its full height, the trunk continues to grow by adding annual rings of new wood to the outside of the trunk, beneath the bark. Typically the cross-sectional surface area (and hence volume and mass as height is now constant) of new wood added each year remains approximately constant for a mature tree. (It is well known that it varies from year to year according to environment, but the average rate is more-or-less fixed). In the end, their is not enough new wood added to encompass the trunk and parts of the tree start to die back and eventually the tree enters decline.

Thus, for a mature tree, the rate of increase in mass per unit time (dM/dt) is essentially constant and the growth equation becomes:

The plot shows the growth rate (this time given the symbol G) as a function of mass. This relative growth declines, as the yearly addition of mass represents a diminishing fraction of the tree's mass. (The units of mass in this plot are arbitrary).

Actual growth curves have been obtained for trees by taking measurements. For the yew tree, one of the longest tree species (of which a number of specimens are dated to around 3000 to 5000 years of age) the following was obtained (by measuring trees up to 1000 years of age):

This matches our picture of slowing relative growth, though in the case of the yew this growth can continue for a remarkably long period of time!

Equation 6 - The Diffusion Equation and Branching Patterns

The diffusion equation is important in modeling the diffusion of carbon dioxide in to leaves where it can be utilised for photosynthesis. The equation is given below:

For many situations we need to use computers to solve this equation by numerical approximation. (We have done this for a simple 1D case in our article on diffusion). This requires certain specialist techniques. An interesting study carried out on sponges used the diffusion equation to model the delivery of food to a sponge. Sponges are animals, but they often assume tree-like growth forms. They draw currents of water through their bodies and filter particles of food, such as bacteria, from these currents. In still waters, diffusion (and also sedimentation due to gravity) must replenish the food supply (clearly the circulating currents generated by the sponge assist but for simplicity let us consider only diffusion). The water is drawn in through pores scattered over the body surface. Areas of the sponge compete with one-another for food - one area may deplete the local region of water of food which an adjacent area needs. By growing in response to food availability (and perhaps a genetic program) the sponge avoids this wasteful competition by branching in such a way that each branch is supplied by the water around it (which in turn is supplied by diffusion from the water column). Branching ensures maximum utilisation of the nutrients without producing tissues in regions depleted of food.

In the case of green plants, the leaves have to absorb carbon dioxide for photosynthesis. The final branching pattern must ensure that leaves do not overlap their regions of supply too much, or else leaf tissue is surplus to requirements and investing in tissues is expensive, especially if those tissues consume more than they produce. There are a couple of dozen or so models of tree branching. Such models can be predicted from theoretical considerations, such as the need to obtain carbon dioxide, and trees will generally fit one of these models, though not all models may have real-life examples. Complications arise because a tree also needs to consider the optimum interception of light by the leaves, the amount of material used in branch and twig construction and mechanical strength. These patterns are sometimes quite precise, but often local environmental conditions will modify the pattern, as a branch responds to local light levels (e.g. shading by a neighbouring plant) mechanical stresses, e.g. due to wind, and damage, e.g. by grazing animals. Click here for more information on tree branching patterns.

Branching is not just confined to the woody parts of trees. Leaves may themselves become sub-divided into leaflets or lobes. Much of this dividing up of leaves is probably again governed by the need to acquire carbon dioxide, though in some cases temperature regulation of the leaf may also be a factor: divided leaves may have better air-circulation for cooling. It is worth recalling that leaves are not generally rigidly attached, but are attached via a flexible hinge called the pulvinus. This allows leaves to flitter in the breeze, especially in such plants like aspen, in which the slightest breeze will flutter the leaves with a very audible sound. This may serve to mix the air, bringing in more carbon dioxide. In static air, a zone of carbon dioxide depletion will accumulate around the leaves (the still boundary layer) and this would then be replenished by the slow process of diffusion only. Stirring the air may serve tor educe the thickness of this still boundary layer. Mechanical factors also need to be taken into account. A flexible leaf offers less resistance to wind, reducing loading on the branch and stem of the tree. Larger leaves are especially divided, such as the compound leaves of horse chestnut (Aesculus hippocastanum) and this again reduces resistance to wind.

A more dissected leaf, by reducing the boundary layer thickness, also increases cooling by advection and evaporation and increases access to carbon dioxide and, probably more importantly, increases the efficient use of carbon dioxide as explained above. The submerged leaves of aquatic plants are often very divided and feathery and this may correlate to the slower diffusion of carbon dioxide in water, making carbon dioxide more limiting under water. Models with the diffusion equation ought to be able to test this idea. Many plants have basal shade leaves with entire (undivided) margins whilst at the top of the stem, the leaves are more divided and called 'sun leaves' and their may be transitional leaves in between. Some have considered this a cooling mechanism to protect upper leaves from overheating in sunlight. However, sun leaves presumably undergo more photosynthesis and so utilise more carbon dioxide, in which case a divided morphology is to be expected. Again, models using the diffusion equation could examine these issues.

Dehydration is another factor affecting leaf morphology. Conifers often thrive in cold habitats in which leaves may suffer ice damage and also in which the plants may experience water stress since much of the water may be locked up as ice: icy environments are dry environments (xerophytic). Thus, a pine tree has narrow leaves which offer less surface area to reduce water loss by evapotranspiration, covered with thick cuticles to again reduce water loss. These needles also shed snow more easily, reducing mechanical loading on the branches and trunk.

Article updated: 15 Sep 2020, 16 Sep 2020