| Electromagnetism and Particle Paths |


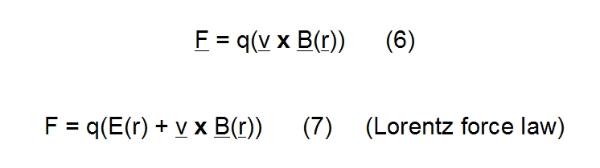
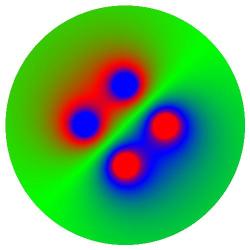
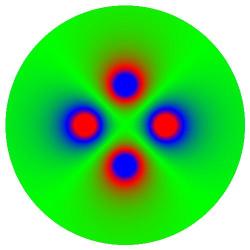
Above: potential energy plots for arrangements of 4 charges - 2 positive charges (red centres) and 2
negative charges (blue centres) of equal magnitude. On this scale green represents zero potential, such
as the points at which the negative and positive charge potentials cancel.
negative charges (blue centres) of equal magnitude. On this scale green represents zero potential, such
as the points at which the negative and positive charge potentials cancel.
The Electric Force - Electrostatics
Electromagnetic forces are fundamental to many
physical processes, including atomic/sub-atomic
and astrophysical processes.
These plots show the potential energy field
around point charges. On the top-left we have a
single (positive) charge. The RGB scale shows
the highest charge region in red, the lowest in
blue and the algorithm used highlights the
contours (equipotentials).
On the top-right, two positive charges are shown
in an orange-blue scale.
Electromagnetic forces are fundamental to many
physical processes, including atomic/sub-atomic
and astrophysical processes.
These plots show the potential energy field
around point charges. On the top-left we have a
single (positive) charge. The RGB scale shows
the highest charge region in red, the lowest in
blue and the algorithm used highlights the
contours (equipotentials).
On the top-right, two positive charges are shown
in an orange-blue scale.
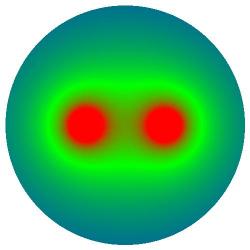
On the bottom-left are two positive charges in
RGB, illustrating a common equipotential, in
green, enclosing both charges.
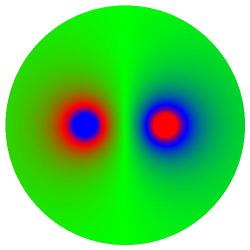
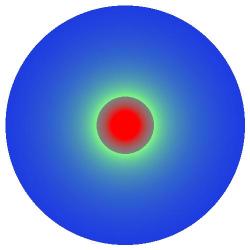
On the bottom-right a positive charge (red
centre) is shown opposite a negative charge
(blue centre) of equal magnitude. On this RGB
scale green illustrates values close to zero,
where the positive and negative potentials
cancel one-another.
Remember electric charge comes in two
'flavours' - negative (-) and positive and like
charges (- and - or + and +) repel whereas
opposite charges (- and + or + and -) attract!
RGB, illustrating a common equipotential, in
green, enclosing both charges.
On the bottom-right a positive charge (red
centre) is shown opposite a negative charge
(blue centre) of equal magnitude. On this RGB
scale green illustrates values close to zero,
where the positive and negative potentials
cancel one-another.
Remember electric charge comes in two
'flavours' - negative (-) and positive and like
charges (- and - or + and +) repel whereas
opposite charges (- and + or + and -) attract!
The charged particles in this plot will tend to move so as to occupy regions of low potential - the two particles of like charge
(above left) are essentially sitting on a 'hill' and will tend to 'roll-away' or move apart from one-another. The particles of
opposite charges, above right, will tend to be attracted to the region of low potential between them - unlike charges attract!
Electric charges are surrounded by electric fields which exert forces on other nearby electric charges. The electric force, F, is
the product of the electric charge, q, and the electric field strength, E (equation 1 below). The electric field strength is then
force per unit of charge (equation 2) meaning the force experienced on a unit test-charge placed in the electric field due to a
second, central charge. If we are dealing with stationary charges (electrostatics) then the electric force between two such point
charges is also called the Coulomb force. The strength of the force decreases by an inverse-square law, meaning that as
distance from the source charge is doubled, the force drops to a quarter of its strength. (This is evident from equation 3, as F
is inversely proportional to r^2, where r is the distance from the central charge, or equivalently, the separation between the
charges). Epsilon-zero, the curly 'e' with the zero subscript, is the permittivity of free space ( = 8.854 x 10^-12 C^2N^-1m^-2) or
the ease with which the electric field traverses a vacuum and its value depends on the choice of units. The r-hat is a unit vector
- force has magnitude and direction and this unit-vector indicates the direction of the force, which depends on the sign of the
charge. The total force due to a collection of charges is equal to the spatial summation of the contributions to the force of each
individual charge (equation 4).
(above left) are essentially sitting on a 'hill' and will tend to 'roll-away' or move apart from one-another. The particles of
opposite charges, above right, will tend to be attracted to the region of low potential between them - unlike charges attract!
Electric charges are surrounded by electric fields which exert forces on other nearby electric charges. The electric force, F, is
the product of the electric charge, q, and the electric field strength, E (equation 1 below). The electric field strength is then
force per unit of charge (equation 2) meaning the force experienced on a unit test-charge placed in the electric field due to a
second, central charge. If we are dealing with stationary charges (electrostatics) then the electric force between two such point
charges is also called the Coulomb force. The strength of the force decreases by an inverse-square law, meaning that as
distance from the source charge is doubled, the force drops to a quarter of its strength. (This is evident from equation 3, as F
is inversely proportional to r^2, where r is the distance from the central charge, or equivalently, the separation between the
charges). Epsilon-zero, the curly 'e' with the zero subscript, is the permittivity of free space ( = 8.854 x 10^-12 C^2N^-1m^-2) or
the ease with which the electric field traverses a vacuum and its value depends on the choice of units. The r-hat is a unit vector
- force has magnitude and direction and this unit-vector indicates the direction of the force, which depends on the sign of the
charge. The total force due to a collection of charges is equal to the spatial summation of the contributions to the force of each
individual charge (equation 4).
The plots shown on this page do not plot the force, nor the field strength, since these are vector fields and we would
have to indicate direction as well as magnitude, so, for simplicity, we have plotted the electric potential, phi, given by
equation 5. The vector r, is our position vector (extending from the coordinate origin to any given point we are
interested in) and the vector ri is the position vector to the centre of charge i and we sum the potential of each of our i
charges, 1,2,...i.
have to indicate direction as well as magnitude, so, for simplicity, we have plotted the electric potential, phi, given by
equation 5. The vector r, is our position vector (extending from the coordinate origin to any given point we are
interested in) and the vector ri is the position vector to the centre of charge i and we sum the potential of each of our i
charges, 1,2,...i.
Electric Force on Moving Charges
If we have a beam of moving charges, such as a beam of electrons (each of which has a mass M and negative charge of
magnitude q) moving between two charged metal plates, then the beam will be deflected toward the plate of opposite
charge (opposite charges attract!).
If we have a beam of moving charges, such as a beam of electrons (each of which has a mass M and negative charge of
magnitude q) moving between two charged metal plates, then the beam will be deflected toward the plate of opposite
charge (opposite charges attract!).
oppositely charged plates, from the left, is attracted to the positive
plate towards which the beam is deflected, and repelled by the
negative plate. A beam of positive particles will be deflected toward the
uppermost positive plate.
In B, a beam of negative particles is again deflected toward the positive
plate, which is on the top in this case; a positive beam would deflect
downwards in this case.
A beam of neutral particles, like neutrons, which carry no net electric
charge, will not be deflected toward either plate in either case.
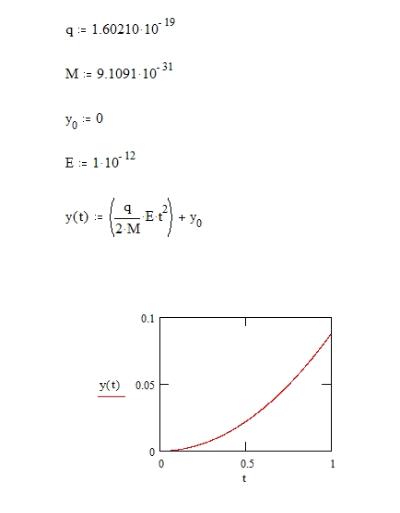
If we calculate the trajectory of such particles, then we find that we
have a situation analogous to a projectile moving in a gravitational field
- the particles follow a parabolic trajectory.
This phenomenon is exploited in the cathode-ray tube.
plate towards which the beam is deflected, and repelled by the
negative plate. A beam of positive particles will be deflected toward the
uppermost positive plate.
In B, a beam of negative particles is again deflected toward the positive
plate, which is on the top in this case; a positive beam would deflect
downwards in this case.
A beam of neutral particles, like neutrons, which carry no net electric
charge, will not be deflected toward either plate in either case.
If we calculate the trajectory of such particles, then we find that we
have a situation analogous to a projectile moving in a gravitational field
- the particles follow a parabolic trajectory.
This phenomenon is exploited in the cathode-ray tube.
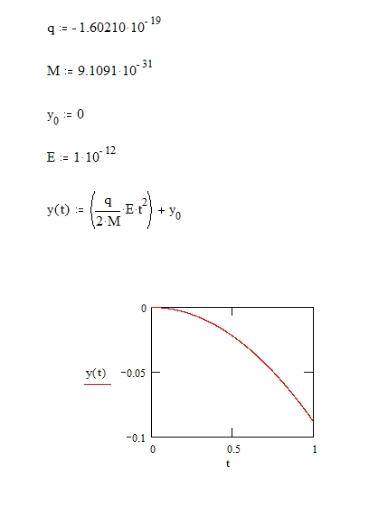
Mathcad calculation of the trajectory of a beam of
negative electrons passing between two charged plates,
with the positively charged plate lowermost (as in case A
above) - beam deflected toward positive plate:
negative electrons passing between two charged plates,
with the positively charged plate lowermost (as in case A
above) - beam deflected toward positive plate:
Mathcad calculation of the trajectory of a beam of positive
particles with the same mass and magnitude of charge as
electrons (such as a beam of positrons or antimatter electrons)
between the same plates as in case A above - beam deflects
toward negative plate:
particles with the same mass and magnitude of charge as
electrons (such as a beam of positrons or antimatter electrons)
between the same plates as in case A above - beam deflects
toward negative plate:
The Magnetic Force
Magnetism has some similarities to the electric force and the two are intimately connected. Like the electric force,
magnetism appears to have two 'flavours' - opposite poles of two bar magnets (north and south magnetic poles) will
attract each other, whilst like poles repel. Moving electric charge generates a magnetic field and a magnetic field will
accelerate moving electric charges. One key difference is that the magnetic force is the vector cross-product
between velocity of the charged particle and the magnetic field strength, B, multiplied by the electric charge (equation
6) - compare this with equation 1 for the electric force. This vector cross-product means that the force acts in a
direction which is at right-angles (perpendicular) to the direction of movement of the particle (given by the velocity
vector) and the magnetic field. If both electric and magnetic forces act upon a particle, then the total force is given by
the Lorentz force law (equation 7).
Magnetism has some similarities to the electric force and the two are intimately connected. Like the electric force,
magnetism appears to have two 'flavours' - opposite poles of two bar magnets (north and south magnetic poles) will
attract each other, whilst like poles repel. Moving electric charge generates a magnetic field and a magnetic field will
accelerate moving electric charges. One key difference is that the magnetic force is the vector cross-product
between velocity of the charged particle and the magnetic field strength, B, multiplied by the electric charge (equation
6) - compare this with equation 1 for the electric force. This vector cross-product means that the force acts in a
direction which is at right-angles (perpendicular) to the direction of movement of the particle (given by the velocity
vector) and the magnetic field. If both electric and magnetic forces act upon a particle, then the total force is given by
the Lorentz force law (equation 7).
Motion of Charged Particles in Magnetic Fields
To calculate the trajectory of a charged particle moving in a
magnetic field, we need a coordinate system for our vectors!
On the left is the scheme I used here - assuming a uniform
magnetic field acting along the x-axis, in the direction of the
positive x-axis (blue arrow) and a particle moving in the
xy-plane (the z-component of the particle's velocity is set = 0)
we can define the angle, theta, between the particle trajectory
and the magnetic field (x-axis) as positive or negative, as
indicated, and restrict the angle to be between -90 <= 0 <=
+90, for purposes of illustration.
The Mathcad worksheet below calculates the particle's
trajectory, which is a helix as the particle 'corkscrews' around a
magnetic field line (taken as the field line along the x-axis):
To calculate the trajectory of a charged particle moving in a
magnetic field, we need a coordinate system for our vectors!
On the left is the scheme I used here - assuming a uniform
magnetic field acting along the x-axis, in the direction of the
positive x-axis (blue arrow) and a particle moving in the
xy-plane (the z-component of the particle's velocity is set = 0)
we can define the angle, theta, between the particle trajectory
and the magnetic field (x-axis) as positive or negative, as
indicated, and restrict the angle to be between -90 <= 0 <=
+90, for purposes of illustration.
The Mathcad worksheet below calculates the particle's
trajectory, which is a helix as the particle 'corkscrews' around a
magnetic field line (taken as the field line along the x-axis):
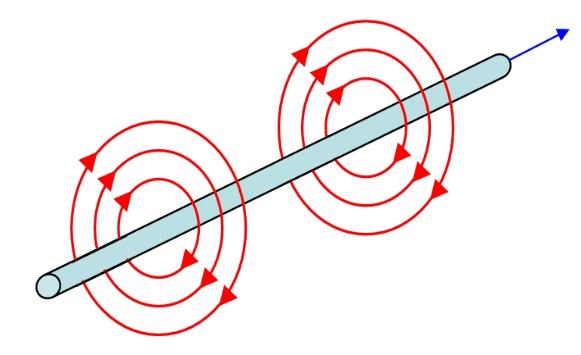
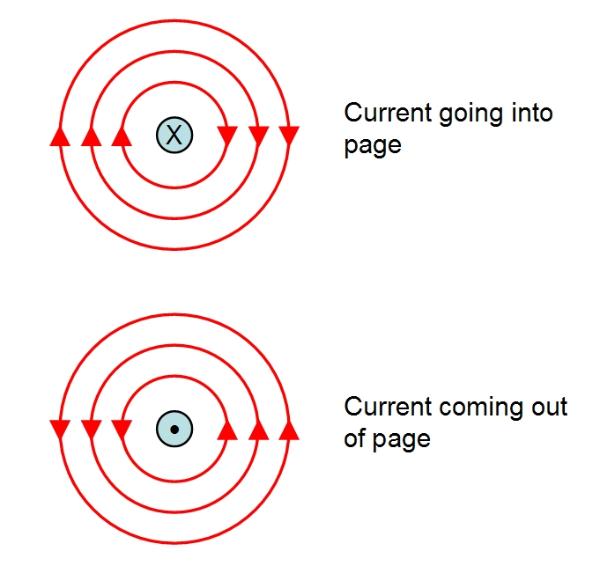
An example of a magnetic field is illustrated below: electric charge (taken as positive by convention, though in reality it is the
negative electrons which move in the opposite direction) flowing in an electrical wire as shown by the blue arrow generates a
magnetic field which loops around the wire in the direction shown (red circular arrows).
negative electrons which move in the opposite direction) flowing in an electrical wire as shown by the blue arrow generates a
magnetic field which loops around the wire in the direction shown (red circular arrows).
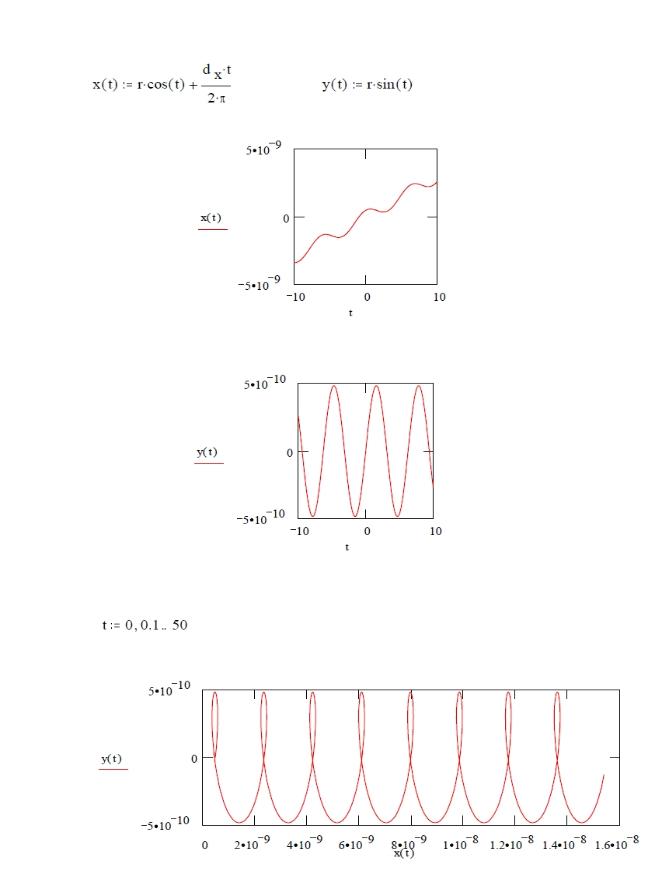
The radius of gyration, the radius of the helix, is given by r; P is the period (time taken) for the electron to complete one
revolution of the helix and dx is the distance moved along the x-axis during one complete turn. The trajectory is plotted below
using parametric equations (parameter t) with the radius of the helix in the y(t) direction. Distance dx depends on the
x-component of velocity (this is the velocity component parallel to B and this does not change) and if this is zero, then the
particle traces a stationary circle. In this case, the trajectory is a helix along the x-axis.
revolution of the helix and dx is the distance moved along the x-axis during one complete turn. The trajectory is plotted below
using parametric equations (parameter t) with the radius of the helix in the y(t) direction. Distance dx depends on the
x-component of velocity (this is the velocity component parallel to B and this does not change) and if this is zero, then the
particle traces a stationary circle. In this case, the trajectory is a helix along the x-axis.
The gyrofrequency, or the number of turns per second, is given by 1/P. According to classical physics, an accelerating
charged particle (remember that in physics acceleration can be a change in speed or a change in direction) emits
electromagnetic radiation ('light') as photons (particles of light). Note that the frequency of radiation emitted = qB/2(pi)M,
particle. This emission of radiation causes the gyrating particle to lose energy - it slows down and so the radius of the orbit
decreases (the frequency remains unchanged) and in reality the radius of the spiral diminishes as the particle moves - the
helix spirals down. This can be seen in the pathway of charged particles in particle detectors. The radiation emitted is also
known as cyclotron radiation.
Note also, that if the sign of the electric charge on the particle is changed, then the sense of the helix is changed. Looking
along the helix from the origin the direction of B (positive x-axis in this case) a negatively charged particle is seen to spiral
clockwise whilst a positively charged particle spirals anti-clockwise. In this way, the sign of the electric charge on the
particle can be determined by analysing its path in a particle detector (such as a bubble chamber).
Cyclotron radiation is seen in the magnetospheres of some planets where charged particles get trapped as they spiral
along the planet's magnetic field, and also in stars, like the Sun and some neutron stars in X-ray pulsars. This radiation is
circularly polarised and has non-thermal characteristics (thermal electromagnetic radiation is emitted by hot matter and has
a different frequency distribution or spectrum).
If the particles are moving at relativistic speeds (that is at speeds close to the speed of light, c = 2.998 x 10^8 m/s) then the
properties of the emitted radiation differ and this radiation is known as synchrotron radiation. This kind of radiation is
often beamed in the direction of particle motion and has non-thermal characteristics. Synchrotron radiation is emitted by
many quasar nuclei - the nuclei of active galaxies that are thought to contain supermassive black holes (at the very least
they do contain very strange objects!). This radiation is highly polarised. Charged particles trapped in the intense magnetic
fields associated with black holes become accelerated to speeds approaching that of light!
charged particle (remember that in physics acceleration can be a change in speed or a change in direction) emits
electromagnetic radiation ('light') as photons (particles of light). Note that the frequency of radiation emitted = qB/2(pi)M,
particle. This emission of radiation causes the gyrating particle to lose energy - it slows down and so the radius of the orbit
decreases (the frequency remains unchanged) and in reality the radius of the spiral diminishes as the particle moves - the
helix spirals down. This can be seen in the pathway of charged particles in particle detectors. The radiation emitted is also
known as cyclotron radiation.
Note also, that if the sign of the electric charge on the particle is changed, then the sense of the helix is changed. Looking
along the helix from the origin the direction of B (positive x-axis in this case) a negatively charged particle is seen to spiral
clockwise whilst a positively charged particle spirals anti-clockwise. In this way, the sign of the electric charge on the
particle can be determined by analysing its path in a particle detector (such as a bubble chamber).
Cyclotron radiation is seen in the magnetospheres of some planets where charged particles get trapped as they spiral
along the planet's magnetic field, and also in stars, like the Sun and some neutron stars in X-ray pulsars. This radiation is
circularly polarised and has non-thermal characteristics (thermal electromagnetic radiation is emitted by hot matter and has
a different frequency distribution or spectrum).
If the particles are moving at relativistic speeds (that is at speeds close to the speed of light, c = 2.998 x 10^8 m/s) then the
properties of the emitted radiation differ and this radiation is known as synchrotron radiation. This kind of radiation is
often beamed in the direction of particle motion and has non-thermal characteristics. Synchrotron radiation is emitted by
many quasar nuclei - the nuclei of active galaxies that are thought to contain supermassive black holes (at the very least
they do contain very strange objects!). This radiation is highly polarised. Charged particles trapped in the intense magnetic
fields associated with black holes become accelerated to speeds approaching that of light!
Download Mathcad 7 Professional worksheet
on trajectories in uniform electric fields.
on trajectories in uniform electric fields.
The Earth has a magnetic field with a strength ranging between 0.3 to 0.6 gauss in strength at the Earth's surface. The
Earth acts like a giant bar magnet - it has a magnetic north pole (near to its geometric South Pole) and a magnetic
south pole (near to its geometric North Pole). Magnetic field lines connect these two poles in large hoops which
collectively form a doughnut-shaped (toroidal or torus-shaped) magnetic field around the Earth, which diminishes in
strength as we travel away from the Earth's surface into space. The magnetic field lines are illustrated in orange in the
above diagram. The blue line represents the Earth's axis of spin, on which lie its geometric poles, and the magnetic
field is tilted about 12 degrees relative to this spin-axis (though the field drifts and its angle of tilt changes noticeably
every year).
Magnetic field lines point from magnetic north to magnetic south - they have to be assigned direction, since the
trajectory followed by electrically charged particles (the helices as illustrated above) depends on this direction. Electric
field lines similarly have direction - radiating out from a positive charge and inwards to a negative charge (so a positive
test charge will follow the field lines). One key difference, however, is that although it is easy to have a single electric
charge, positive or negative, it is very hard, if not impossible, to have a single isolated magnetic pole (a monopole) and
with a few possible extreme exceptions, a magnetic north is always accompanied by a magnetic south (a dipole).
The presence of the Earth's magnetic field is thought to be due to electric charges flowing in the Earth's outer core,
which appears to be a metallic liquid. Rotation of the Earth sets up currents of moving charges inside this outer core
and these charges generate a magnetic field. If the field is sufficiently strong, then the charges will be confined by it, as
they gyrate along the magnetic field lines, and the field is reinforced and achieves a fairly stable pattern - this is the
electromagnetic dynamo theory.
There is an additional complication to the shape of the Earth's magnetic field further from the surface - it gets distorted
by the Solar wind and in the lee-side it is drawn out into a comet-shaped tail as it ploughs against the wind. The region
dominated by the magnetic field is called the magnetosphere and this extends up to a boundary with the oncoming
Solar wind, a boundary called the magnetopause.
Within 8 - 10 times the radius of the Earth from the earth's surface, the field is dipolar and largely symmetrical, as
illustrated, but beyond this the magnetopause is reached on the sunward side and the leeward magnetic tail extends
more than 1000 Earth radii away into space, pointing away from the Sun.
The Solar wind contains plasma - atoms stripped of electrons, resulting in a gas of ions, protons and electrons. Some
of these particles leak through the magnetopause and become trapped in the Earth's magnetic field - gyrating along
the magnetic field lines. These particles will gyrate around the arc of a field-line, travelling away from one pole and
toward the other. This is fine where the magnetic field-lines are more or less parallel to one-another, as above the
equator (a so-called uniform magnetic field) but towards the poles, the field-lines converge and get squeezed together.
Particles gyrating along the field-lines into these regions experience another phenomenon - they are reflected to travel
back along the field-lines in the opposite direction from which they came. Thus they bounce around between northern
and southern latitudes, traveling as far poleward as they can before they are reflected, gyrating as they go. Additional
charged particles in the magnetosphere come from the Earth's own ionosphere - cosmic rays colliding with air
molecules generate atom-fragments: ions, protons and electrons.
Such an arrangement where converging filed lines reflect charged particles is called a magnetic mirror. The result is
that the particles remain trapped in torus-shaped belts some distance above the equator - these are the Van Allen
radiation belts:
Earth acts like a giant bar magnet - it has a magnetic north pole (near to its geometric South Pole) and a magnetic
south pole (near to its geometric North Pole). Magnetic field lines connect these two poles in large hoops which
collectively form a doughnut-shaped (toroidal or torus-shaped) magnetic field around the Earth, which diminishes in
strength as we travel away from the Earth's surface into space. The magnetic field lines are illustrated in orange in the
above diagram. The blue line represents the Earth's axis of spin, on which lie its geometric poles, and the magnetic
field is tilted about 12 degrees relative to this spin-axis (though the field drifts and its angle of tilt changes noticeably
every year).
Magnetic field lines point from magnetic north to magnetic south - they have to be assigned direction, since the
trajectory followed by electrically charged particles (the helices as illustrated above) depends on this direction. Electric
field lines similarly have direction - radiating out from a positive charge and inwards to a negative charge (so a positive
test charge will follow the field lines). One key difference, however, is that although it is easy to have a single electric
charge, positive or negative, it is very hard, if not impossible, to have a single isolated magnetic pole (a monopole) and
with a few possible extreme exceptions, a magnetic north is always accompanied by a magnetic south (a dipole).
The presence of the Earth's magnetic field is thought to be due to electric charges flowing in the Earth's outer core,
which appears to be a metallic liquid. Rotation of the Earth sets up currents of moving charges inside this outer core
and these charges generate a magnetic field. If the field is sufficiently strong, then the charges will be confined by it, as
they gyrate along the magnetic field lines, and the field is reinforced and achieves a fairly stable pattern - this is the
electromagnetic dynamo theory.
There is an additional complication to the shape of the Earth's magnetic field further from the surface - it gets distorted
by the Solar wind and in the lee-side it is drawn out into a comet-shaped tail as it ploughs against the wind. The region
dominated by the magnetic field is called the magnetosphere and this extends up to a boundary with the oncoming
Solar wind, a boundary called the magnetopause.
Within 8 - 10 times the radius of the Earth from the earth's surface, the field is dipolar and largely symmetrical, as
illustrated, but beyond this the magnetopause is reached on the sunward side and the leeward magnetic tail extends
more than 1000 Earth radii away into space, pointing away from the Sun.
The Solar wind contains plasma - atoms stripped of electrons, resulting in a gas of ions, protons and electrons. Some
of these particles leak through the magnetopause and become trapped in the Earth's magnetic field - gyrating along
the magnetic field lines. These particles will gyrate around the arc of a field-line, travelling away from one pole and
toward the other. This is fine where the magnetic field-lines are more or less parallel to one-another, as above the
equator (a so-called uniform magnetic field) but towards the poles, the field-lines converge and get squeezed together.
Particles gyrating along the field-lines into these regions experience another phenomenon - they are reflected to travel
back along the field-lines in the opposite direction from which they came. Thus they bounce around between northern
and southern latitudes, traveling as far poleward as they can before they are reflected, gyrating as they go. Additional
charged particles in the magnetosphere come from the Earth's own ionosphere - cosmic rays colliding with air
molecules generate atom-fragments: ions, protons and electrons.
Such an arrangement where converging filed lines reflect charged particles is called a magnetic mirror. The result is
that the particles remain trapped in torus-shaped belts some distance above the equator - these are the Van Allen
radiation belts:
There are two such belts - an inner belt (shown in cyan) which sits about 1.5 earth radii above the Earth's surface, and
the outer belt (shown in magenta) at about 3.5 earth radii. These toroidal belts follow the contours of the magnetic
field:
the outer belt (shown in magenta) at about 3.5 earth radii. These toroidal belts follow the contours of the magnetic
field:
The inner belt contains higher energy particles - protons with around 50 MeV of energy or more and 30 MeV plus
electrons.
Electronvolt: the kinetic energy gained by an electron in 'falling' through a potential difference of 1 volt.
electrons.
Electronvolt: the kinetic energy gained by an electron in 'falling' through a potential difference of 1 volt.
| 1 eV = 1 electron volt = 1.602e-19 J 1 MeV = 1 mega electron volt = 1 million eV |
When the field-lines converge towards the poles, this indicates a strengthening of the magnetic field in this region. This
causes the gyrating particles to gyrate in smaller orbits (radius of orbit, r is inversely proportional to B) and in such a
non-uniform magnetic field the speed of the particles along the field-lines does change - it slows down (the right-hand
rule indicates a force acting against the path of the helix). However, magnetic fields cannot alter the total speed of
particles, as they cannot change the particles' kinetic energy, thus as the particles move slower and slower in the
direction of the field line, they move faster and faster in their circular orbits. Eventually, the particles execute tiny
stationary orbits at high speed and stop moving along the field-line and then their path reverses. In the Van Allen belts,
the particles oscillate back-and-forth between the poles once every 0.1-3 seconds!
In addition to bouncing back-and-forth between the polar regions, the particles also drift in longitude (the field strength
diminishes with distance from the Earth and eventually the field-lines become too weak to confine the particles which can
then move from one field-line to another. High-energy protons drift westward around the Earth every 0.1 s and
lower-energy electrons drift eastward, circling the Earth once every 1 to 10 hours. These velocities are quite fantastic!
The Aurorae
The inner radiation belt interacts with the Earth's upper atmosphere - lower energy electrons drop-out and collide with
air molecules, exciting and ionising the molecules. As the molecules de-excite they emit the excess-energy they gained
in the collision as photons of light - the frequency and colour of the photons depends upon the element excited (mostly
nitrogen or oxygen) and the flickering curtains of light produced in the upper atmosphere are known as the aurora
borealis, or northern lights in northern latitudes, and the aurora australis, or southern lights, in southern latitudes.
These lights occur at altitudes between 80 and 1000 km. The Solar wind influences the aurorae - if the Solar wind
increases in strength then it may supply more electrons to the Van Allen belts and it may also disturb the magnetic field,
causing electrons to be dumped from the inner belt into the atmosphere - both effects will increase the aurorae.
The Nature of Magnetism - it's all relative!
Magnetism and electric phenomena are intimately connected, and yet it seems easier intuitively to understand electric
charges and their electrical interactions than to conceptualise magnetism. Magnetism seems especially mysterious,
however, it is only relative! Consider electrons flowing in an electric wire, from one 'end' of the wire to the other. These
moving electrons generate a magnetic field around the wire. Now consider a second wire with electrons flowing through
it. Bring the two wires near to each other - how will the magnetic fields interact?
If the wires are parallel (side-by-side) and their currents flow in the same direction, then the wires will become attracted
to one-another. Reverse the direction of flow of current in one of the two wires, so that the two currents flow in opposite
directions, and the wires will repel one-another - like currents attract, unlike currents repel. It is as if the wires acquire
net electric charge!
Consider just one wire again. Imagine the electrons flowing from left to right along the wire and now imagine an electron
outside the wire and flowing in the same direction and with the same speed as the electrons in the wire. This is like two
wires with like currents - the electron will be attracted toward the wire. As opposite charges attract, and the electron is
negatively charged, it as if the wire had somehow gained a net positive charge! Wires are made of metal, and metal
atoms are electrically neutral - metals consist of a sea of delocalised electrons bathing a lattice of positive ions, but
overall the net charge is zero. (For bonding in metals see bonding in the chemical archives). How can this be? The wire
still has a zero net electric charge!
If the external electron is 'seeing' more positive charge in the wire, then it as if the number of positive ions (atom cores)
per unit length of wire had somehow increased! This could happen if the wire shrank and became shorter without
effecting the flowing electrons - this would increase the density of positive ions in the wire, without increasing the total
number - more positive charges cannot appear since electric charge is conserved - the net charge on the wire must
remain zero and does so! Clearly and experimenter in the lab would not see the wire shrink! That's because length is
relative!
From the point of view of the electrons moving along, it is the wire that appears to be moving past them in the opposite
direction. According to the Theory of Special Relativity moving objects become shorter in the direction of their motion.
However, motion is relative - to the electrons the wire is moving and so the wire shrinks, but to the wire the electrons are
moving and so they shrink and become closer together. Thus the electron 'sees' the wire shrink and increase its positive
charge density and so the electron is attracted toward the wire by the electric force of attraction. The wire 'sees' the
distance between the electrons shorten, increasing electron charge density and the positive wire is attracted to this
apparent increase in negative charge by the electric force. The end result is that the wire and electron are attracted to
one-another (but since the wire is much heavier it moves less and an experimenter in the lab will see the electron move
toward the wire).
The conclusion is surprising - electricity and magnetism are manifestations of the same fundamental force, the
electromagnetic force, as seen from different points of view!
causes the gyrating particles to gyrate in smaller orbits (radius of orbit, r is inversely proportional to B) and in such a
non-uniform magnetic field the speed of the particles along the field-lines does change - it slows down (the right-hand
rule indicates a force acting against the path of the helix). However, magnetic fields cannot alter the total speed of
particles, as they cannot change the particles' kinetic energy, thus as the particles move slower and slower in the
direction of the field line, they move faster and faster in their circular orbits. Eventually, the particles execute tiny
stationary orbits at high speed and stop moving along the field-line and then their path reverses. In the Van Allen belts,
the particles oscillate back-and-forth between the poles once every 0.1-3 seconds!
In addition to bouncing back-and-forth between the polar regions, the particles also drift in longitude (the field strength
diminishes with distance from the Earth and eventually the field-lines become too weak to confine the particles which can
then move from one field-line to another. High-energy protons drift westward around the Earth every 0.1 s and
lower-energy electrons drift eastward, circling the Earth once every 1 to 10 hours. These velocities are quite fantastic!
The Aurorae
The inner radiation belt interacts with the Earth's upper atmosphere - lower energy electrons drop-out and collide with
air molecules, exciting and ionising the molecules. As the molecules de-excite they emit the excess-energy they gained
in the collision as photons of light - the frequency and colour of the photons depends upon the element excited (mostly
nitrogen or oxygen) and the flickering curtains of light produced in the upper atmosphere are known as the aurora
borealis, or northern lights in northern latitudes, and the aurora australis, or southern lights, in southern latitudes.
These lights occur at altitudes between 80 and 1000 km. The Solar wind influences the aurorae - if the Solar wind
increases in strength then it may supply more electrons to the Van Allen belts and it may also disturb the magnetic field,
causing electrons to be dumped from the inner belt into the atmosphere - both effects will increase the aurorae.
The Nature of Magnetism - it's all relative!
Magnetism and electric phenomena are intimately connected, and yet it seems easier intuitively to understand electric
charges and their electrical interactions than to conceptualise magnetism. Magnetism seems especially mysterious,
however, it is only relative! Consider electrons flowing in an electric wire, from one 'end' of the wire to the other. These
moving electrons generate a magnetic field around the wire. Now consider a second wire with electrons flowing through
it. Bring the two wires near to each other - how will the magnetic fields interact?
If the wires are parallel (side-by-side) and their currents flow in the same direction, then the wires will become attracted
to one-another. Reverse the direction of flow of current in one of the two wires, so that the two currents flow in opposite
directions, and the wires will repel one-another - like currents attract, unlike currents repel. It is as if the wires acquire
net electric charge!
Consider just one wire again. Imagine the electrons flowing from left to right along the wire and now imagine an electron
outside the wire and flowing in the same direction and with the same speed as the electrons in the wire. This is like two
wires with like currents - the electron will be attracted toward the wire. As opposite charges attract, and the electron is
negatively charged, it as if the wire had somehow gained a net positive charge! Wires are made of metal, and metal
atoms are electrically neutral - metals consist of a sea of delocalised electrons bathing a lattice of positive ions, but
overall the net charge is zero. (For bonding in metals see bonding in the chemical archives). How can this be? The wire
still has a zero net electric charge!
If the external electron is 'seeing' more positive charge in the wire, then it as if the number of positive ions (atom cores)
per unit length of wire had somehow increased! This could happen if the wire shrank and became shorter without
effecting the flowing electrons - this would increase the density of positive ions in the wire, without increasing the total
number - more positive charges cannot appear since electric charge is conserved - the net charge on the wire must
remain zero and does so! Clearly and experimenter in the lab would not see the wire shrink! That's because length is
relative!
From the point of view of the electrons moving along, it is the wire that appears to be moving past them in the opposite
direction. According to the Theory of Special Relativity moving objects become shorter in the direction of their motion.
However, motion is relative - to the electrons the wire is moving and so the wire shrinks, but to the wire the electrons are
moving and so they shrink and become closer together. Thus the electron 'sees' the wire shrink and increase its positive
charge density and so the electron is attracted toward the wire by the electric force of attraction. The wire 'sees' the
distance between the electrons shorten, increasing electron charge density and the positive wire is attracted to this
apparent increase in negative charge by the electric force. The end result is that the wire and electron are attracted to
one-another (but since the wire is much heavier it moves less and an experimenter in the lab will see the electron move
toward the wire).
The conclusion is surprising - electricity and magnetism are manifestations of the same fundamental force, the
electromagnetic force, as seen from different points of view!